GraphAssortativity

GraphAssortativity[g]

gives the assortativity coefficient of a graph g using vertex degrees.

GraphAssortativity[g,"prop"]

gives the assortativity coefficient of the graph g using vertex property "prop".

GraphAssortativity[g,{{vi 1,vi 2,…},…}]

gives the assortativity coefficient of the graph g with respect to the vertex partition {{vi 1,vi 2,…},…}.

GraphAssortativity[g,{v1,v2,…}{x1,x2,…}]

gives the assortativity coefficient of the graph g using data {x1,x2,…} for vertices {v1,v2,…}.

GraphAssortativity[{vw,…},…]

uses rules vw to specify the graph g.

Details and Options

  • For a graph with 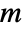edges and adjacency matrix entries 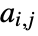, the assortativity coefficient is given by 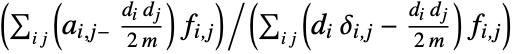, where 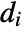is the out-degree for the vertex vi and 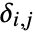is 1 if there is an edge from vi to vj and 0 otherwise.
  • For quantitative data where x1,x2,… are used, 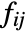is taken to be xixj.
  • For categorical data where x1,x2,… are used, 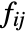is taken to be 1 if xi and xj are equal and 0 otherwise.
  • In GraphAssortativity[g], xi is taken to be the vertex out-degree for the vertex vi.
  • In GraphAssortativity[g,"prop"], xi is taken to be AnnotationValue[{g,vi},"prop"] for the vertex vi.
  • In GraphAssortativity[g,{{vi 1,vi 2,…},…}], vertices in a subset {vi 1,vi 2,…} have the same categorical data xi 1=xi 2=….
  • GraphAssortativity[g,Automatic->{x1,x2,…}] takes the vertex list to be VertexList[g].
  • The option "DataType"->type can be used to specify the type for the data x1,x2,…. Possible settings are "Quantitative" and "Categorical".
  • The option "Normalized"->False can be used to compute the assortativity modularity.
  • For a graph with 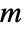edges and adjacency matrix entries 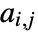, the assortativity modularity is given by 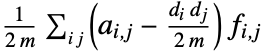, where 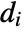is the out-degree for the vertex vi.
  • GraphAssortativity works with undirected graphs, directed graphs, weighted graphs, multigraphs, and mixed graphs.

Examples

open allclose all

Basic Examples  (2)

Compute the assortativity coefficient of the Zachary karate club network:

Distribution of the assortativity coefficient of uniform random graphs:

Scope  (12)

GraphAssortativity works with undirected graphs:

Directed graphs:

Weighted graphs:

Multigraphs:

Mixed graphs:

Use rules to specify the graph:

Compute the assortativity coefficient using vertex property data:

A vertex partition:

A specified dataset:

A partition or assignment of a subset of VertexList:

GraphAssortativity works with symbolic expressions:

GraphAssortativity works with large graphs:

Applications  (3)

Compare the assortativity coefficient of vertex partitions by vertex color:

Disassortativity by number of friends in a friendship network:

A partition of the network shows assortative mixing:

A friendship network at a high school, with vertices color coded by race. Analyze the preference for students to associate with others who are similar:

Highly social students are friends with other highly social students:

Positive tendency for students to associate with others of the same race:

Properties & Relations  (2)

The assortativity coefficient is between -1 and 1:

Perfect assortative graph:

Completely disassortative graph:

GraphAssortativity is Pearson correlation coefficient of degree between connected vertices:

Correlation gives the Pearson correlation coefficient:

Wolfram Research (2012), GraphAssortativity, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphAssortativity.html (updated 2015).

Text

Wolfram Research (2012), GraphAssortativity, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphAssortativity.html (updated 2015).

CMS

Wolfram Language. 2012. "GraphAssortativity." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GraphAssortativity.html.

APA

Wolfram Language. (2012). GraphAssortativity. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphAssortativity.html

BibTeX

@misc{reference.wolfram_2024_graphassortativity, author="Wolfram Research", title="{GraphAssortativity}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GraphAssortativity.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_graphassortativity, organization={Wolfram Research}, title={GraphAssortativity}, year={2015}, url={https://reference.wolfram.com/language/ref/GraphAssortativity.html}, note=[Accessed: 21-December-2024 ]}