GraphDisjointUnion

GraphDisjointUnion[g1,g2]

gives the graph disjoint union of the graphs g1 and g2.

GraphDisjointUnion[g1,g2,…]

gives the disjoint union of g1, g2, ….

GraphDisjointUnion[{vw,…},…]

uses rules vw to specify the graph g.

Details and Options

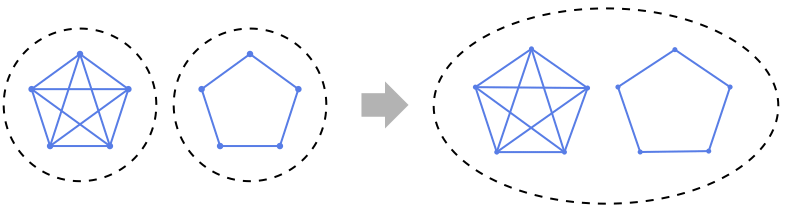
Background & Context

  • GraphDisjointUnion gives a new graph obtained from two or more directed or undirected graphs obtained by separately taking the unions of the original vertex and edge sets. For edges with same vertex labels in different graphs, GraphDisjointUnion keeps all of them, but uniquely relabels vertices. GraphDisjointUnion therefore corresponds to the usual meaning of “graph union” in graph theoretical parlance. The resulting graph has canonically indexed vertices with labels from 1 to the sum of initial graph vertex counts. The particular labeling of the resulting graph may therefore depend on the ordering of vertices in the original graph and on the order in which the original graphs are specified, but differently labeled graphs obtained from GraphDisjointUnion in this way all belong to the same isomorphism class.
  • The adjacency matrix for a disjoint union corresponds to the block diagonal matrix of the original graph adjacency matrices.
  • Related functions include GraphUnion, GraphIntersection, and GraphDifference. Unlike GraphDisjointUnion, GraphUnion keeps only one edge if multiple edges exist in different graphs having the same vertex labels. GraphIntersection gives the graph obtained from the union of vertex sets and intersection of edge sets of the original graphs. GraphDifference gives the graph obtained from the union of vertex sets of two graphs and the complement of the second graph’s edge set with respect to the first. GraphComplement gives the graph that has the same vertex set as a given graph, but with edges corresponding to absent edges in the original (and vice versa).

Examples

open allclose all

Basic Examples  (1)

Obtain the graph disjoint union of two graphs:

Scope  (6)

GraphDisjointUnion works with undirected graphs:

Directed graphs:

Multigraphs:

Mixed graphs:

Use rules to specify the graph:

GraphDisjointUnion works with more than two graphs:

Properties & Relations  (4)

The VertexCount of the graph disjoint union is the total of vertex counts for the graphs:

The EdgeCount of the graph disjoint union is the total edges of the graphs:

The graph disjoint union can be found using GraphUnion:

The adjacency matrix for a disjoint union corresponds to the block diagonal of adjacency matrices:

Wolfram Research (2010), GraphDisjointUnion, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphDisjointUnion.html (updated 2015).

Text

Wolfram Research (2010), GraphDisjointUnion, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphDisjointUnion.html (updated 2015).

CMS

Wolfram Language. 2010. "GraphDisjointUnion." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GraphDisjointUnion.html.

APA

Wolfram Language. (2010). GraphDisjointUnion. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphDisjointUnion.html

BibTeX

@misc{reference.wolfram_2024_graphdisjointunion, author="Wolfram Research", title="{GraphDisjointUnion}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GraphDisjointUnion.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_graphdisjointunion, organization={Wolfram Research}, title={GraphDisjointUnion}, year={2015}, url={https://reference.wolfram.com/language/ref/GraphDisjointUnion.html}, note=[Accessed: 21-December-2024 ]}