is an option to Graph and related functions that specifies what layout to use.


GraphLayout
Listing of Layouts »is an option to Graph and related functions that specifies what layout to use.
Details





- A graph layout is typically computed using several stages. With GraphLayout->{s1->m1,…}, stage si is handled by method mi.
- Possible graph layout stages si are:
-
"VertexLayout" how to embed vertices "EdgeLayout" how to route edges "PackingLayout" how to place connected components of vertices - "VertexLayout" methods include:
-
Automatic automatically select a layout None do not compute a layout "emb" named embedding - Possible special embeddings "emb" include:
-

"BipartiteEmbedding" vertices on two parallel lines 
"CircularEmbedding" vertices on a circle 
"CircularMultipartiteEmbedding" vertices on segments of a circle 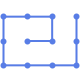
"DiscreteSpiralEmbedding" vertices on a discrete spiral 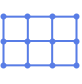
"GridEmbedding" vertices on a grid 
"LinearEmbedding" vertices on a line 
"MultipartiteEmbedding" vertices on several parallel lines 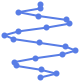
"SpiralEmbedding" vertices on a 3D spiral projected to 2D 
"StarEmbedding" vertices on a circle with a center - Possible structured embeddings "emb" for layered graphs such as trees and directed acyclic graphs include:
-

"BalloonEmbedding" vertices on a circle with the center at the parent vertex 
"RadialEmbedding" vertices on a circular segment 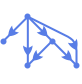
"LayeredDigraphEmbedding" vertices on parallel lines for directed acyclic graphs 
"LayeredEmbedding" vertices on parallel lines 
"SymmetricLayeredEmbedding" vertices on symmetric parallel lines 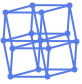
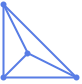
"HyperbolicRadialEmbedding" vertices on a circular segment on the Poincaré disk - Possible optimizing embeddings "emb" all minimize a quantity and include:
-
"GravityEmbedding" energy with vertices as mass points and edges as springs 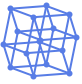
"HighDimensionalEmbedding" energy for spring-electrical in high dimension 
"PlanarEmbedding" number of edge crossings 
"SpectralEmbedding" weighted sum of squares distances 
"SphericalEmbedding" energy with vertices on a sphere and edges as springs 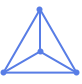
"SpringElectricalEmbedding" energy with edges as springs and vertices as charges 
"SpringEmbedding" energy with edges as springs 
"TutteEmbedding" number of edge crossings and distance to neighbors 
"HyperbolicSpringEmbedding" energy with edges as springs on the Poincaré disk - "EdgeLayout" methods include:
-
"DividedEdgeBundling" divide edges into segments bundle "HierarchicalEdgeBundling" bundle edges following a hierarchical tree structure "StraightLine" straight lines between edges - "PackingLayout" methods include:
-
"ClosestPacking" approximate closest packing from the top left "ClosestPackingCenter" approximate closest packing from the center "Layered" arrange in layers starting at the top left "LayeredLeft" arrange in layers starting at the left "LayeredTop" arrange in layers starting at the top "NestedGrid" arrange on a nested grid
Examples
open all close allBasic Examples (2)
Scope (131)
Basic Use (3)
Vertex Layout (116)
"BalloonEmbedding" (8)
Place each vertex in an enclosing circle centered at its parent vertex:
"BalloonEmbedding" works best for tree graphs:
Use the option "EvenAngle"->True to place vertices evenly in an enclosing circle:
With the setting "OptimalOrder"->True, the vertex ordering optimizes the angular resolution and the aspect ratio:
Use the option "RootVertex"->v to set the root vertex:
Use the option "Rotation"->r to rotate the layout:
"BipartiteEmbedding" (2)
Place vertices on two vertical lines based on a bipartite partition:
"BipartiteEmbedding" works for bipartite graphs only:
"CircularEmbedding" (4)
"CircularEmbedding" works best for circulant graphs, LCF notation embeddings and cycle graphs:
Use the option "Offset"->offset to specify the offset angles:
With the setting "OptimalOrder"->True, vertices are reordered so that they lie nicely on a circle:
"CircularMultipartiteEmbedding" (3)
Place vertices on polygon lines based on a vertex partition:
"CircularMultipartiteEmbedding" works best for k-partite graphs:
Use "VertexPartition"->partition to specify a partition of vertices:
"DiscreteSpiralEmbedding" (3)
Place vertices on a discrete spiral:
"DiscreteSpiralEmbedding" works best for path graphs:
With the setting "OptimalOrder"->True, vertices are reordered so that they lie nicely on a discrete spiral:
"GravityEmbedding" (2)
"GridEmbedding" (3)
"GridEmbedding" works best for grid graphs:
"HighDimensionalEmbedding" (3)
Place vertices in high dimension according to spring-electrical embedding and project down:
"HighDimensionalEmbedding" works best for large graphs:
Use "RandomSeed"->int to specify a seed for the random number generator that computes the initial vertex placement:
"HyperbolicRadialEmbedding" (4)
Place vertices on a Poincaré disk.
"HyperbolicRadialEmbedding" works best for tree graphs:
"HyperbolicSpringEmbedding" (10)
Place vertices on a Poincaré disk:
"HyperbolicSpringEmbedding" works best tree graphs:
With the setting "EdgeWeighted"True, edge weights are used:
Use the option "EnergyControl"e to specify limitations on the total energy of the system during minimization:
Use "InferentialDistance"d to specify a cutoff distance beyond which the interaction between vertices is assumed to be nonexistent:
Use "MaxIteration"it to specify a maximum number of iterations to be used in attempting to minimize the energy:
Use "RandomSeed"int to specify a seed for the random number generator that computes the initial vertex placement:
Use "StepControl"method to define how step length is modified during energy minimization:
Use "StepLength"r to specify the initial step length used in moving the vertices around:
Use "Tolerance"r to specify the tolerance used in terminating the energy minimization process:
"LayeredEmbedding" (7)
Place vertices in several layers in such a way as to minimize edges between nonadjacent layers:
"LayeredEmbedding" works best for tree graphs:
Use the option "LayerSizeFunction"->func to specify the relative height:
Use the option "RootVertex"->v to set the root vertex:
Use the option "LeafDistance"->d to specify the leaf distance:
Use the option "Orientation"->o to draw a tree with different orientations:
"LayeredDigraphEmbedding" (7)
Place vertices in a series of layers:
"LayeredDigraphEmbedding" works best for directed acyclic graphs:
Use the option "RootVertex"->v to set the root vertex:
Use the option "Rotation"r to rotate the layout:
Use the option "Orientation"->o to draw a tree with different orientations:
Use the option "VertexLayerPosition"->positions to specify the positions of layers:
"LinearEmbedding" (2)
"MultipartiteEmbedding" (3)
Place vertices on multiple line grids based on a vertex partition:
"MultipartiteEmbedding" works best for k-partite graphs:
Use "VertexPartition"->partition to specify a partition of vertices:
"PlanarEmbedding" (2)
"RadialEmbedding" (5)
Place vertices in concentric circles:
"RadialEmbedding" works best for tree graphs:
Use the option "RootVertex"->v to set the root vertex:
"SpectralEmbedding" (3)
Place vertices so the weighted sum of squares of mutual distances is minimized:
"SpectralEmbedding" works best for well-structured graphs:
Use the option "RelaxationFactor"->r to get the layout based on a relaxed Laplace matrix:
"SphericalEmbedding" (2)
"SpiralEmbedding" (3)
"SpiralEmbedding" works best for path graphs:
With the setting "OptimalOrder"->True, vertices are reordered so that they lie on the spiral nicely:
"SpringElectricalEmbedding" (15)
Place vertices so that they minimize mechanical and electrical energy when each vertex has a charge and each edge corresponds to a spring:
"SpringElectricalEmbedding" works best for most graphs:
With the setting "EdgeWeighted"->True, edge weights are used:
Use the option "EnergyControl"->e to specify limitations on the total energy of the system during minimization:
Use "InferentialDistance"->d to specify a cutoff distance beyond which the interaction between vertices is assumed to be nonexistent:
Use "MaxIteration"->it to specify a maximum number of iterations to be used in attempting to minimize the energy:
Use "Multilevel"->method to specify a method used during a recursive procedure of coarsening a graph:
With the setting "Octree"->True, an octree data structure (in three dimensions) or a quadtree data structure (in two dimensions) is used in the calculation of repulsive force:
Use "RandomSeed"->int to specify a seed for the random number generator that computes the initial vertex placement:
Use "RepulsiveForcePower"->r to control how fast the repulsive force decays over distance:
Use the option "Rotation"r to rotate the layout:
Use "SpringConstant"r to control the constant in the attractive force:
Use "StepControl"->method to define how step length is modified during energy minimization:
Use "StepLength"->r to specify the initial step length used in moving the vertices around:
Use "Tolerance"->r to specify the tolerance used in terminating the energy minimization process:
"SpringEmbedding" (12)
Place vertices so that they minimize mechanical energy when each edge corresponds to a spring:
"SpringEmbedding" works best for regular structured graphs:
With the setting "EdgeWeighted"->True, edge weights are used:
Use the option "EnergyControl"->e to specify limitations on the total energy of the system during minimization:
Use "InferentialDistance"->d to specify a cutoff distance beyond which the interaction between vertices is assumed to be nonexistent:
Use "MaxIteration"->it to specify a maximum number of iterations to be used in attempting to minimize the energy:
Use "Multilevel"->method to specify a method used during a recursive procedure of coarsening a graph:
Use "RandomSeed"->int to specify a seed for the random number generator that computes the initial vertex placement:
Use the option "Rotation"r to rotate the layout:
Use "StepControl"->method to define how step length is modified during energy minimization:
Use "StepLength"->r to specify the initial step length used in moving the vertices around:
Use "Tolerance"->r to specify the tolerance used in terminating the energy minimization process:
"StarEmbedding" (4)
Place vertices on a star shape:
"StarEmbedding" works best for star-like graphs:
Use the option "Offset"->offset to specify the offset angles:
"SymmetricLayeredEmbedding" (4)
Place vertices in a series of layers symmetrically:
"SymmetricLayeredEmbedding" works best for symmetric directed acyclic graphs:
"TutteEmbedding" (2)
Place vertices without crossing edges and minimize the sum of distances to neighbors:
"TutteEmbedding" works for 3-connected planar graphs only:
Edge Layout (3)
Packing Layout (6)
Applications (2)
Properties & Relations (6)
GraphLayout can be used for general graphs:
VertexCoordinates overrides GraphLayout coordinates:
Use AbsoluteOptions to extract VertexCoordinates computed using a layout algorithm:
See Also
Related Guides
History
Introduced in 2010 (8.0) | Updated in 2012 (9.0) ▪ 2014 (10.0) ▪ 2019 (12.0) ▪ 2021 (12.3) ▪ 2025 (14.2) ▪ 2025 (14.3)
Text
Wolfram Research (2010), GraphLayout, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphLayout.html (updated 2025).
CMS
Wolfram Language. 2010. "GraphLayout." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/GraphLayout.html.
APA
Wolfram Language. (2010). GraphLayout. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphLayout.html
BibTeX
@misc{reference.wolfram_2025_graphlayout, author="Wolfram Research", title="{GraphLayout}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/GraphLayout.html}", note=[Accessed: 14-August-2025]}
BibLaTeX
@online{reference.wolfram_2025_graphlayout, organization={Wolfram Research}, title={GraphLayout}, year={2025}, url={https://reference.wolfram.com/language/ref/GraphLayout.html}, note=[Accessed: 14-August-2025]}