JacobiZeta
JacobiZeta[ϕ,m]
gives the Jacobi zeta function ![]() .
.
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
- The Jacobi zeta function is given in terms of elliptic integrals by
![TemplateBox[{phi, m}, JacobiZeta]=TemplateBox[{phi, m}, EllipticE2]-TemplateBox[{m}, EllipticE]TemplateBox[{phi, m}, EllipticF]/TemplateBox[{m}, EllipticK] TemplateBox[{phi, m}, JacobiZeta]=TemplateBox[{phi, m}, EllipticE2]-TemplateBox[{m}, EllipticE]TemplateBox[{phi, m}, EllipticF]/TemplateBox[{m}, EllipticK]](Files/JacobiZeta.en/2.png) .
. - Argument conventions for elliptic integrals are discussed in "Elliptic Integrals and Elliptic Functions".
- JacobiZeta[ϕ,m] has branch cut discontinuities at
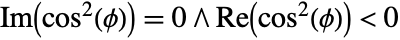 and at
and at 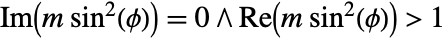 .
. - For certain special arguments, JacobiZeta automatically evaluates to exact values.
- JacobiZeta can be evaluated to arbitrary numerical precision.
- JacobiZeta automatically threads over lists.
- JacobiZeta can be used with Interval and CenteredInterval objects. »
Examples
open allclose allBasic Examples (4)
Scope (30)
Numerical Evaluation (5)
The precision of the output tracks the precision of the input:
Evaluate for complex arguments and parameters:
Evaluate JacobiZeta efficiently at high precision:
JacobiZeta threads elementwise over lists:
JacobiZeta can be used with Interval and CenteredInterval objects:
Specific Values (5)
Simple exact results are generated automatically:
Exact values after FunctionExpand is applied:
Find a local maximum as a root of ![]() :
:
JacobiZeta is an odd function with respect to the first argument:
Visualization (3)
Plot JacobiZeta as a function of its first parameter ![]() :
:
Plot JacobiZeta as a function of its second parameter ![]() :
:
Function Properties (6)
JacobiZeta is not an analytic function:
However, for fixed ![]() ,
, ![]() is an analytic function of
is an analytic function of ![]() :
:
Thus, for example, ![]() has no singularities or discontinuities:
has no singularities or discontinuities:
![]() is neither nondecreasing nor nonincreasing:
is neither nondecreasing nor nonincreasing:
Differentiation and Integration (4)
Series Expansions (4)
Taylor expansion for JacobiZeta:
Plot the first three approximations for ![]() around
around ![]() :
:
Taylor expansion at the origin in the parameter ![]() :
:
Plot the first three approximations for ![]() around
around ![]() :
:
Find series expansions at a branch point:
JacobiZeta can be applied to a power series:
Function Representations (3)
Applications (3)
Plot of the real part of JacobiZeta over the complex plane:
Supersymmetric zero‐energy solution of the Schrödinger equation in a periodic potential:
Check the Schrödinger equation:
Plot the superpotential, the potential and the wave function:
Properties & Relations (5)
Use FunctionExpand to express JacobiZeta in terms of incomplete elliptic integrals:
Some special cases require argument restrictions:
Numerically find a root of a transcendental equation:
For real arguments, if ![]() , then JacobiZN[u,m]JacobiZeta[ϕ,m] for
, then JacobiZN[u,m]JacobiZeta[ϕ,m] for ![]() :
:
JacobiZeta[ϕ,m] is real valued for real arguments subject to ![]() :
:
Possible Issues (4)
Machine-precision input may be insufficient to give a correct answer:
A larger setting for $MaxExtraPrecision may be needed:
JacobiZeta, function ![]() of amplitude
of amplitude ![]() , is not to be confused with JacobiZN, sometimes denoted as
, is not to be confused with JacobiZN, sometimes denoted as ![]() and a function of elliptic argument
and a function of elliptic argument ![]() :
:
The Wolfram Language JacobiZeta[ϕ,m] is a function of amplitude ![]() and uses the following definition:
and uses the following definition:
JacobiZN[u,m] is a function of elliptic argument ![]() and uses the definition
and uses the definition ![]() , where
, where ![]() is JacobiEpsilon[u,m]:
is JacobiEpsilon[u,m]:
To avoid confusion, JacobiZN uses a different TraditionalForm:
Text
Wolfram Research (1991), JacobiZeta, Wolfram Language function, https://reference.wolfram.com/language/ref/JacobiZeta.html (updated 2020).
CMS
Wolfram Language. 1991. "JacobiZeta." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/JacobiZeta.html.
APA
Wolfram Language. (1991). JacobiZeta. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JacobiZeta.html