KuiperTest

KuiperTest[data]

tests whether data is normally distributed using the Kuiper test.

KuiperTest[data,dist]

tests whether data is distributed according to dist using the Kuiper test.

KuiperTest[data,dist,"property"]

returns the value of "property".

Details and Options

  • KuiperTest performs the Kuiper goodness-of-fit test with null hypothesis 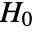that data was drawn from a population with distribution dist and alternative hypothesis 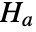that it was not.
  • By default a probability value or 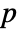-value is returned.
  • A small 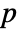-value suggests that it is unlikely that the data came from dist.
  • The dist can be any symbolic distribution with numeric and symbolic parameters or a dataset.
  • The data can be univariate {x1,x2,…} or multivariate {{x1,y1,…},{x2,y2,…},…}.
  • The Kuiper test assumes that the data came from a continuous distribution.
  • The Kuiper test effectively uses a test statistic based on 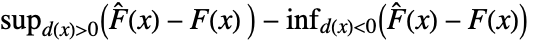where 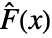is the empirical CDF of data and 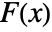is the CDF of dist.
  • For multivariate tests, the sum of the univariate marginal 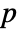-values is used and is assumed to follow a UniformSumDistribution under .
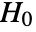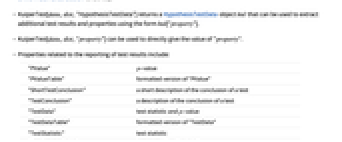
  • KuiperTest[data,dist,"HypothesisTestData"] returns a HypothesisTestData object htd that can be used to extract additional test results and properties using the form htd["property"].
  • KuiperTest[data,dist,"property"] can be used to directly give the value of "property".
  • Properties related to the reporting of test results include:
  • "PValue"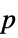-value
    "PValueTable"formatted version of "PValue"
    "ShortTestConclusion"a short description of the conclusion of a test
    "TestConclusion"a description of the conclusion of a test
    "TestData"test statistic and 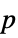-value
    "TestDataTable"formatted version of "TestData"
    "TestStatistic"test statistic
    "TestStatisticTable"formatted "TestStatistic"
  • The following properties are independent of which test is being performed.
  • Properties related to the data distribution include:
  • "FittedDistribution"fitted distribution of data
    "FittedDistributionParameters"distribution parameters of data
  • The following options can be given:
  • Method Automaticthe method to use for computing 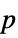-values
    SignificanceLevel0.05cutoff for diagnostics and reporting
  • For a test for goodness-of-fit, a cutoff 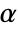is chosen such that 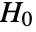is rejected only if 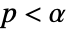. The value of 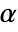used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. By default 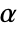is set to 0.05.
  • With the setting Method->"MonteCarlo", 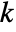datasets of the same length as the input 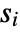are generated under 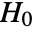using the fitted distribution. The EmpiricalDistribution from KuiperTest[si,dist,"TestStatistic"] is then used to estimate the 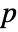-value.

Examples

open allclose all

Basic Examples  (4)

Perform a Kuiper test for normality:

Test the fit of some data to a particular distribution:

Compare the distributions of two datasets:

Extract the test statistic from a Kuiper test:

Scope  (9)

Testing  (6)

Perform a Kuiper test for normality:

The -value for the normal data is large compared to the -value for the non-normal data:

Test the goodness-of-fit to a particular distribution:

Compare the distributions of two datasets:

The two datasets do not have the same distribution:

Test for multivariate normality:

Test for goodness-of-fit to any multivariate distribution:

Create a HypothesisTestData object for repeated property extraction:

The properties available for extraction:

Reporting  (3)

Tabulate the results of the Kuiper test:

The full test table:

A -value table:

The test statistic:

Retrieve the entries from a Kuiper test table for custom reporting:

Report test conclusions using "ShortTestConclusion" and "TestConclusion":

The conclusion may differ at a different significance level:

Options  (3)

Method  (3)

Use Monte Carlo-based methods for a computation formula:

Set the number of samples to use for Monte Carlo-based methods:

The Monte Carlo estimate converges to the true -value with increasing samples:

Set the random seed used in Monte Carlo-based methods:

The seed affects the state of the generator and has some effect on the resulting -value:

Applications  (2)

A power curve for the Kuiper test:

Visualize the approximate power curve:

Estimate the power of the Kuiper test when the underlying distribution is a UniformDistribution[{-4,4}], the test size is 0.05, and the sample size is 12:

Spatial signs transform bivariate data to points on a unit circle and are often used in tests of location. The null hypothesis can be tested by determining whether the spatial signs are significantly clustered:

The spatial sign function:

Clustering occurs for nonzero mean vectors:

A bivariate test for location using spatial signs and Kuiper's test:

The test does not reject when the mean is close to the null value:

The test rejects the null hypothesis when the mean is not close to the null value:

Properties & Relations  (7)

By default, univariate data is compared to a NormalDistribution:

The parameters have been estimated from the data:

Multivariate data is compared to a MultinormalDistribution by default:

The parameters of the test distribution are estimated from the data if not specified:

Specified parameters are not estimated:

Maximum-likelihood estimates are used for unspecified parameters of the test distribution:

If the parameters are unknown, KuiperTest applies a correction when possible:

The parameters are estimated but no correction is applied:

The fitted distribution is the same as before and the -value is corrected:

Independent marginal densities are assumed in tests for multivariate goodness-of-fit:

The test statistic is identical when independence is assumed:

The Kuiper test works with the values only when the input is a TimeSeries:

Possible Issues  (3)

The Kuiper test is not intended for discrete distributions:

The test tends to be quite conservative:

Use Monte Carlo methods or PearsonChiSquareTest in these cases:

The Kuiper test is not valid for some distributions when parameters have been estimated from the data:

Provide parameter values if they are known:

Alternatively, use Monte Carlo methods to approximate the -value:

Ties in the data are ignored:

Differences may be more apparent with larger numbers of ties:

Neat Examples  (1)

Compute the statistic when the null hypothesis is true:

The test statistic given a particular alternative:

Compare the distributions of the test statistics:

Wolfram Research (2010), KuiperTest, Wolfram Language function, https://reference.wolfram.com/language/ref/KuiperTest.html.

Text

Wolfram Research (2010), KuiperTest, Wolfram Language function, https://reference.wolfram.com/language/ref/KuiperTest.html.

CMS

Wolfram Language. 2010. "KuiperTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/KuiperTest.html.

APA

Wolfram Language. (2010). KuiperTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KuiperTest.html

BibTeX

@misc{reference.wolfram_2025_kuipertest, author="Wolfram Research", title="{KuiperTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/KuiperTest.html}", note=[Accessed: 21-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_kuipertest, organization={Wolfram Research}, title={KuiperTest}, year={2010}, url={https://reference.wolfram.com/language/ref/KuiperTest.html}, note=[Accessed: 21-February-2025 ]}