PauliMatrix

PauliMatrix[k]

gives the k^(th) Pauli spin matrix .

Details and Options

  • PauliMatrix gives 2×2 constant matrices with the property .
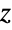  • PauliMatrix[0] and PauliMatrix[4] give the identity matrix.
  • The following options can be given:
  • TargetStructure Automaticthe structure of the returned matrix
    WorkingPrecision Infinityprecision at which to create entries
  • Possible settings for TargetStructure include:
  • Automaticautomatically choose the representation returned
    "Dense"represent the matrix as a dense matrix
    "Hermitian"represent the matrix as a Hermitian matrix
    "Sparse"represent the matrix as a sparse array
    "Unitary"represent the matrix as a unitary matrix
  • With the setting TargetStructureAutomatic, a dense matrix is returned.

Examples

open allclose all

Basic Examples  (1)

Generate Pauli matrices:

Scope  (1)

PauliMatrix threads element-wise over lists:

Options  (6)

TargetStructure  (4)

Return the Pauli matrix as a dense matrix:

Return the Pauli matrix as a sparse array:

Return the Pauli matrix as a Hermitian matrix:

Return the Pauli matrix as a unitary matrix:

WorkingPrecision  (2)

Create a machine-precision Pauli matrix:

Create an arbitrary-precision Pauli matrix:

Applications  (4)

Pauli's differential equation:

Pauli matrices' algebra:

Build a unitary matrix representing the rotation of the spinor around the axis through angle :

Rotation by 360° changes the spinor's direction:

In quantum mechanics, systems with finitely many states are represented by unit vectors and physical quantities by matrices that act on them. Consider a spin-1/2 particle such as an electron in the following state:

The operator for the component of angular momentum is given by the following matrix:

Compute the expected angular momentum in this state as :

The uncertainty in the angular momentum is :

The uncertainty in the component of angular momentum is computed analogously:

The uncertainty principle gives a lower bound on the product of uncertainties, :

Wolfram Research (2008), PauliMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/PauliMatrix.html (updated 2024).

Text

Wolfram Research (2008), PauliMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/PauliMatrix.html (updated 2024).

CMS

Wolfram Language. 2008. "PauliMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/PauliMatrix.html.

APA

Wolfram Language. (2008). PauliMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PauliMatrix.html

BibTeX

@misc{reference.wolfram_2025_paulimatrix, author="Wolfram Research", title="{PauliMatrix}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/PauliMatrix.html}", note=[Accessed: 05-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_paulimatrix, organization={Wolfram Research}, title={PauliMatrix}, year={2024}, url={https://reference.wolfram.com/language/ref/PauliMatrix.html}, note=[Accessed: 05-May-2025 ]}