Permanent

Permanent[m]

gives the permanent of the square matrix m.

Details and Options

  • Permanent works with both numeric and symbolic matrices.
  • The permanent of an 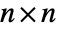matrix m is given by 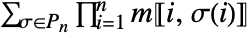, where the 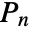are the permutations of 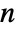elements.

Examples

open all close all

Basic Examples  (1)

Find the permanent of symbolic matrices:

In[1]:=
Click for copyable input
Out[1]=
In[2]:=
Click for copyable input
Out[2]=

Scope  (1)

Applications  (3)

Properties & Relations  (4)

Possible Issues  (1)

Introduced in 2015
(10.2)