"ImplicitRungeKutta" Method for NDSolve
Introduction
Implicit Runge–Kutta methods have a number of desirable properties.
The Gauss–Legendre methods, for example, are self-adjoint, meaning that they provide the same solution when integrating forward or backward in time.
Coefficients
A generic framework for implicit Runge–Kutta methods has been implemented. The focus so far is on methods with interesting geometric properties and currently covers the following schemes:
The derivation of the method coefficients can be carried out to arbitrary order and arbitrary precision.
Coefficient Generation
- Start with the definition of the polynomial, defining the abscissas of the
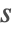 stage coefficients. For example, the abscissas for Gauss–Legendre methods are defined as
stage coefficients. For example, the abscissas for Gauss–Legendre methods are defined as 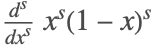 .
.
- Univariate polynomial factorization gives the underlying irreducible polynomials defining the roots of the polynomials.
- Root objects are constructed to represent the solutions (using unique root isolation and Jenkins–Traub for the numerical approximation).
- Root objects are then approximated numerically for precision coefficients.
- Condition estimates for Vandermonde systems governing the coefficients yield the precision to take in approximating the roots numerically.
- Specialized solvers for nonconfluent Vandermonde systems are then used to solve equations for the coefficients (see [GVL96]).
- One step of iterative refinement is used to polish the approximate solutions and to check that the coefficients are obtained to the requested precision.
Examples
The "ImplicitSolver" method of "ImplicitRungeKutta" has options AccuracyGoal and PrecisionGoal that specify the absolute and relative error to aim for in solving the nonlinear system of equations.
These options have the same default values as the corresponding options in NDSolve, since often there is little point in solving the nonlinear system to much higher accuracy than the local error of the method.
The first invariant is the Hamiltonian of the system, and the error is now bounded, as it should be, since the Gauss implicit Runge–Kutta method is a symplectic integrator.
This defines the implicit midpoint method as the one-stage implicit Runge–Kutta method of order two.
At present, the implicit Runge–Kutta method framework does not use banded Newton techniques for uncoupling the nonlinear system.
Option Summary
"ImplicitRungeKutta" Options
option name | default value | |
| "Coefficients" | "ImplicitRungeKuttaGaussCoefficients" | specify the coefficients to use in the implicit Runge–Kutta method |
| "DifferenceOrder" | Automatic | specify the order of local accuracy of the method |
| "ImplicitSolver" | "Newton" | specify the solver to use for the nonlinear system; valid settings are FixedPoint or "Newton" |
| "StepSizeControlParameters" | Automatic | specify the step control parameters |
| "StepSizeRatioBounds" | { | specify the bounds on a relative change in the new step size |
| "StepSizeSafetyFactors" | Automatic | specify the safety factors to use in the step size estimate |
Options of the method "ImplicitRungeKutta".
The default setting of Automatic for the option "StepSizeSafetyFactors" uses the values {9/10,9/10}.
"ImplicitSolver" Options
option name | default value | |
| AccuracyGoal | Automatic | specify the absolute tolerance to use in solving the nonlinear system |
| "IterationSafetyFactor" | specify the safety factor to use in solving the nonlinear system | |
| MaxIterations | Automatic | specify the maximum number of iterations to use in solving the nonlinear system |
| PrecisionGoal | Automatic | specify the relative tolerance to use in solving the nonlinear system |
Common options of "ImplicitSolver".
option name | default value | |
| "JacobianEvaluationParameter" | specify when to recompute the Jacobian matrix in Newton iterations | |
| "LinearSolveMethod" | Automatic | specify the linear solver to use in Newton iterations |
| "LUDecompositionEvaluationParameter" | specify when to compute LU decompositions in Newton iterations |
Options specific to the "Newton" method of "ImplicitSolver".