Stiffness Detection
| Overview | "NonstiffTest" Method Option |
| Introduction | Examples |
| Linear Stability | Option Summary |
| "StiffnessTest" Method Option |
Overview
Many differential equations exhibit some form of stiffness, which restricts the step size and hence effectiveness of explicit solution methods.
A number of implicit methods have been developed over the years to circumvent this problem.
For the same step size, implicit methods can be substantially less efficient than explicit methods, due to the overhead associated with the intrinsic linear algebra.
This cost can be offset by the fact that, in certain regions, implicit methods can take substantially larger step sizes.
Several attempts have been made to provide user-friendly codes that automatically attempt to detect stiffness at runtime and switch between appropriate methods as necessary.
A number of strategies that have been proposed to automatically equip a code with a stiffness detection device are outlined here.
Particular attention is given to the problem of estimation of the dominant eigenvalue of a matrix in order to describe how stiffness detection is implemented in NDSolve.
Numerical examples illustrate the effectiveness of the strategy.
Initialization
Introduction
Consider the numerical solution of initial value problems:
Stiffness is a combination of problem, solution method, initial condition and local error tolerances.
Stiffness limits the effectiveness of explicit solution methods due to restrictions on the size of steps that can be taken.
Stiffness arises in many practical systems as well as in the numerical solution of partial differential equations by the method of lines.
Example
The Van der Pol oscillator is a non-conservative oscillator with nonlinear damping and is an example of a stiff system of ordinary differential equations:
The method "StiffnessSwitching" uses a pair of extrapolation methods by default:
Solution
Stiffness can often occur in regions that follow rapid transients.
The problem is that when the solution is changing rapidly, there is little point using a stiff solver, since local accuracy is the dominant issue.
For efficiency, it would be useful if the method could automatically detect regions where local accuracy (and not stability) is important.
Linear Stability
Linear stability theory arises from the study of Dahlquist's scalar linear test equation:
as a simplified model for studying the initial value problem (1).
Stability is characterized by analyzing a method applied to (2) to obtain
where ![]() and
and ![]() is the (rational) stability function.
is the (rational) stability function.
The boundary of absolute stability is obtained by considering the region:
Explicit Euler Method
The explicit or forward Euler method
The shaded region represents instability, where ![]() >1.
>1.
The linear stability boundary (LSB) is often taken as the intersection with the negative real axis.
For the explicit Euler method ![]() .
.
For an eigenvalue of ![]() , linear stability requirements mean that the step size needs to satisfy
, linear stability requirements mean that the step size needs to satisfy ![]() , which is a very mild restriction.
, which is a very mild restriction.
However, for an eigenvalue of ![]() , linear stability requirements mean that the step size needs to satisfy
, linear stability requirements mean that the step size needs to satisfy ![]() , which is a very severe restriction.
, which is a very severe restriction.
Example
This example shows the effect of stiffness on the step size sequence when using an explicit Runge-Kutta method to solve a stiff system.
Implicit Euler Method
The implicit or backward Euler method:
The method is unconditionally stable for the entire left half-plane.
This means that to maintain stability there is no longer a restriction on the step size.
The drawback is that an implicit system of equations now has to be solved at each integration step.
Type Insensitivity
A type-insensitive solver recognizes and responds efficiently to stiffness at each step and so is insensitive to the (possibly changing) type of the problem.
One of the most established solvers of this class is LSODA [H83], [P83].
Later generations of LSODA such as CVODE no longer incorporate a stiffness detection device. The reason is because LSODA uses norm bounds to estimate the dominant eigenvalue and these bounds, as will be seen later, can be quite inaccurate.
The low order of A(α)-stable BDF methods means that LSODA and CVODE are not very suitable for solving systems with high accuracy or systems where the dominant eigenvalue has a large imaginary part. Alternative methods, such as those based on extrapolation of linearly implicit schemes, do not suffer from these issues.
Much of the work on stiffness detection was carried out in the 1980s and 1990s using standalone FORTRAN codes.
New linear algebra techniques and efficient software have since become available and these are readily accessible in the Wolfram Language.
Stiffness can be a transient phenomenon, so detecting nonstiffness is equally important [S77], [B90].
"StiffnessTest" Method Option
There are several approaches that can be used to switch from a nonstiff to a stiff solver.
Direct Estimation
A convenient way of detecting stiffness is to directly estimate the dominant eigenvalue of the Jacobian ![]() of the problem (see [S77], [P83], [S83], [S84a], [S84c], [R87] and [HW96]).
of the problem (see [S77], [P83], [S83], [S84a], [S84c], [R87] and [HW96]).
Such an estimate is often available as a by-product of the numerical integration and so it is reasonably inexpensive.
If ![]() denotes an approximation to the eigenvector corresponding to the dominant eigenvalue of the Jacobian, with
denotes an approximation to the eigenvector corresponding to the dominant eigenvalue of the Jacobian, with ![]() sufficiently small, then by the mean value theorem a good approximation to the leading eigenvalue is
sufficiently small, then by the mean value theorem a good approximation to the leading eigenvalue is
Richardson's extrapolation provides a sequence of refinements that yields a quantity of this form, as do certain explicit Runge–Kutta methods.
Cost is at most two function evaluations, but often at least one of these is available as a by-product of the numerical integration, so it is reasonably inexpensive.
Let ![]() denote the linear stability boundary—the intersection of the linear stability region with the negative real axis.
denote the linear stability boundary—the intersection of the linear stability region with the negative real axis.
The product ![]() gives an estimate that can be compared to the linear stability boundary of a method in order to detect stiffness:
gives an estimate that can be compared to the linear stability boundary of a method in order to detect stiffness:
Description
The methods "DoubleStep", "Extrapolation", and "ExplicitRungeKutta" have the option "StiffnessTest", which can be used to identify whether the method applied with the specified AccuracyGoal and PrecisionGoal tolerances to a given problem is stiff.
The method option "StiffnessTest" itself accepts a number of options that implement a weak form of (5) where the test is allowed to fail a specified number of times.
The reason for this is that some problems can be only mildly stiff in a certain region and an explicit integration method may still be efficient.
"NonstiffTest" Method Option
The "StiffnessSwitching" method has the option "NonstiffTest", which is used to switch back from a stiff method to a nonstiff method.
The following settings are allowed for the option "NonstiffTest":
Switching to a Nonstiff Solver
An approach that is independent of the stiff method is used.
Given the Jacobian J (or an approximation), compute one of:
Many linear algebra techniques focus on solving a single problem to high accuracy.
For stiffness detection, a succession of problems with solutions to one or two digits is adequate.
For a numerical discretization
consider a sequence ![]() of matrices in some sub-interval(s)
of matrices in some sub-interval(s)
The spectra of the succession of matrices often change very slowly from step to step.
The goal is to find a way of estimating (bounds on) dominant eigenvalues of ![]() succession of matrices
succession of matrices ![]() that:
that:
NormBound
A simple and efficient technique of obtaining a bound on the dominant eigenvalue is to use the norm of the Jacobian ![]() where typically
where typically ![]() or
or ![]() .
.
The method has complexity ![]() , which is less than the work carried out in the stiff solver.
, which is less than the work carried out in the stiff solver.
This is the approach used by LSODA.
The setting "NormBound" of the option "NonstiffTest" computes ![]() and
and ![]() and returns the smaller of the two values.
and returns the smaller of the two values.
Example
Direct Eigenvalue Computation
For small problems (![]() ) it can be efficient just to compute the dominant eigenvalue directly.
) it can be efficient just to compute the dominant eigenvalue directly.
The setting "Direct" of the option "NonstiffTest" computes the dominant eigenvalue of ![]() using the same LAPACK routines as Eigenvalues.
using the same LAPACK routines as Eigenvalues.
For larger problems the cost of direct eigenvalue computation is ![]() , which becomes prohibitive when compared to the cost of the linear algebra work in a stiff solver.
, which becomes prohibitive when compared to the cost of the linear algebra work in a stiff solver.
A number of iterative schemes have been implemented for this purpose. These effectively work by approximating the dominant eigenspace in a smaller subspace and using dense eigenvalue methods for the smaller problem.
The Power Method
Shampine has proposed the use of the power method for estimating the dominant eigenvalue of the Jacobian [S91].
The power method is perhaps not a very well-respected method, but has received a resurgence of interest due to its use in Google's page ranking.
The power method can be used when
Description
Given a starting vector ![]() , compute
, compute
The Rayleigh quotient is used to compute an approximation to the dominant eigenvalue:
In practice, the approximate eigenvector is scaled at each step:
Properties
The power method converges linearly with rate
In particular, the method does not converge when applied to a matrix with a dominant complex conjugate pair of eigenvalues.
Generalizations
The power method can be adapted to overcome the issue of equimodular eigenvalues (e.g. NAPACK).
However the modification does not generally address the issue of the slow rate of convergence for clustered eigenvalues.
There are two main approaches to generalizing the power method:
Although the methods work quite differently, there are a number of core components that can be shared and optimized.
Subspace and Krylov iteration cost ![]() operations.
operations.
They project an ![]()
![]() matrix to an
matrix to an ![]()
![]() matrix, where
matrix, where ![]() .
.
The small matrix represents the dominant eigenspace and approximation uses dense eigenvalue routines.
Subspace Iteration
Subspace (or simultaneous) iteration generalizes the ideas in the power method by acting on m vectors at each step.
Start with an orthonormal set of vectors ![]() , where usually
, where usually ![]() :
:
Form the product with the matrix ![]() :
:
In order to prevent all vectors from converging to multiples of the same dominant eigenvector ![]() of
of ![]() , they are orthonormalized:
, they are orthonormalized:
The orthonormalization step is expensive compared to the matrix product.
Rayleigh–Ritz Projection
Input: matrix ![]() and an orthonormal set of vectors
and an orthonormal set of vectors ![]()
The matrix S has small dimension ![]()
![]() .
.
Note that the Schur decomposition can be computed in real arithmetic when ![]() using a quasi upper triangular matrix
using a quasi upper triangular matrix ![]() .
.
Convergence
Subspace (or simultaneous) iteration generalizes the ideas in the power method by acting on ![]() vectors at each step.
vectors at each step.
SRRIT converges linearly with rate
In particular, the rate for the dominant eigenvalue is
Therefore it can be beneficial to take, for example, ![]() or more even if we are only interested in the dominant eigenvalue.
or more even if we are only interested in the dominant eigenvalue.
Error Control
A relative error test on successive approximations' dominant eigenvalue is
This is not sufficient since it can be satisfied when convergence is slow.
If ![]() or
or ![]() then the
then the ![]() th column of
th column of ![]() is not uniquely determined.
is not uniquely determined.
The residual test used in SRRIT is:
where ![]() ,
, ![]() is the
is the ![]() th column of
th column of ![]() , and
, and ![]() is the
is the ![]() th column of
th column of ![]() .
.
This is advantageous since it works for equimodular eigenvalues.
The first column position of the upper triangular matrix ![]() is tested because of the use of an ordered Schur decomposition.
is tested because of the use of an ordered Schur decomposition.
Implementation
There are several implementations of subspace iteration.
- LOPSI [SJ81]
- Schur Rayleigh–Ritz iteration [BS97]
"An attractive feature of SRRIT is that it displays monotonic consistency, that is, as the convergence tolerance decreases so does the size of the computed residuals" [LS96].
SRRIT makes use of an ordered Schur decomposition where eigenvalues of the largest modulus appear in the upper-left entries.
Modified Gram–Schmidt with reorthonormalization is used to form ![]() , which is faster than Householder transformations.
, which is faster than Householder transformations.
The approximate dominant subspace ![]() at integration time
at integration time ![]() is used to start the iteration at the next integration step
is used to start the iteration at the next integration step ![]() :
:
KrylovIteration
Given an ![]()
![]() matrix
matrix ![]() whose columns
whose columns ![]() comprise an orthogonal basis of a given subspace
comprise an orthogonal basis of a given subspace ![]() :
:
The Rayleigh–Ritz procedure consists of computing ![]() and solving the associated eigenproblem
and solving the associated eigenproblem ![]() .
.
The approximate eigenpairs of the original problem ![]() ,
, ![]() satisfy
satisfy ![]() and
and ![]() , which are called Ritz values and Ritz vectors.
, which are called Ritz values and Ritz vectors.
The process works best when the subspace ![]() approximates an invariant subspace of
approximates an invariant subspace of ![]() .
.
This process is effective when ![]() is equal to the Krylov subspace associated with a matrix
is equal to the Krylov subspace associated with a matrix ![]() and a given initial vector
and a given initial vector ![]() as
as
Description
The method of Arnoldi is a Krylov-based projection algorithm that computes an orthogonal basis of the Krylov subspace and produces a projected ![]()
![]() matrix
matrix ![]() with
with ![]() .
.
Input: matrix ![]() , the number of steps
, the number of steps ![]() , an initial vector
, an initial vector ![]() of norm 1.
of norm 1.
In the case of Arnoldi, ![]() has an unreduced upper Hessenberg form (upper triangular with an additional nonzero subdiagonal).
has an unreduced upper Hessenberg form (upper triangular with an additional nonzero subdiagonal).
Orthogonalization is usually carried out by means of a Gram–Schmidt procedure.
The quantities computed by the algorithm satisfy
The residual ![]() gives an indication of proximity to an invariant subspace and the associated norm
gives an indication of proximity to an invariant subspace and the associated norm ![]() indicates the accuracy of the computed Ritz pairs:
indicates the accuracy of the computed Ritz pairs:
Restarting
The Ritz pairs converge quickly if the initial vector ![]() is rich in the direction of the desired eigenvalues.
is rich in the direction of the desired eigenvalues.
When this is not the case then a restarting strategy is required in order to avoid excessive growth in both work and memory.
There are several strategies for restarting, in particular:
- Implicit restart—a new starting vector is formed from the Arnoldi process combined with an implicitly shifted QR algorithm.
Explicit restart is relatively simple to implement, but implicit restart is more efficient since it retains the relevant eigeninformation of the larger problem. However implicit restart is difficult to implement in a numerically stable way.
An alternative that is much simpler to implement, but achieves the same effect as implicit restart, is a Krylov–Schur method [S01].
Implementation
A number of software implementations are available, in particular:
- ARPACK [ARPACK98]
- SLEPc [SLEPc05]
The implementation in "NonstiffTest" is based on Krylov–Schur iteration.
Automatic Strategy
The "Automatic" setting uses an amalgamation of the methods as follows.
- For
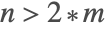 subspace iteration is used with a default basis size of
subspace iteration is used with a default basis size of 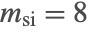 . If the method succeeds then the resulting basis is used to start the method at the next integration step.
. If the method succeeds then the resulting basis is used to start the method at the next integration step.
- If subspace iteration fails to converge after
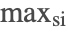 iterations then the dominant vector is used to start the Krylov method with a default basis size of
iterations then the dominant vector is used to start the Krylov method with a default basis size of  . Subsequent integration steps use the Krylov method, starting with the resulting vector from the previous step.
. Subsequent integration steps use the Krylov method, starting with the resulting vector from the previous step.
- If Krylov iteration fails to converge after
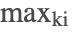 iterations, then norm bounds are used for the current step. The next integration step will continue to try to use Krylov iteration.
iterations, then norm bounds are used for the current step. The next integration step will continue to try to use Krylov iteration.
- Since they are so inexpensive, norm bounds are always computed when subspace or Krylov iteration is used and the smaller of the absolute values is used.
Step Rejections
Caching of the time of evaluation ensures that the dominant eigenvalue estimate is not recomputed for rejected steps.
Stiffness detection is also performed for rejected steps since:
Iterative Method Options
The iterative methods of "NonstiffTest" have options that can be modified:
The default tolerance aims for just one correct digit, but often obtains substantially more accurate values—especially after a few successful iterations at successive steps.
The default values limiting the number of iterations are:
If these values are set too large then a convergence failure becomes too costly.
In difficult problems, it is better to share the work of convergence across steps. Since the methods effectively refine the basis vectors from the previous step, there is a reasonable chance of convergence in subsequent steps.
Latency and Switching
It is important to incorporate some form of latency in order to avoid a cycle where the "StiffnessSwitching" method continually tries to switch between stiff and nonstiff methods.
The options "MaxRepetitions" and "SafetyFactor" of "StiffnessTest" and "NonstiffTest" are used for this purpose.
The default settings allow switching to be quite reactive, which is appropriate for one-step integration methods.
- "StiffnessTest" is carried out at the end of a step with a nonstiff method. When either value of the option "MaxRepetitions" is reached, a step rejection occurs and the step is recomputed with a stiff method.
- "NonstiffTest" is preemptive. It is performed before a step is taken with a stiff solve using the Jacobian matrix from the previous step.
Examples
Van der Pol
StiffnessTest
NonstiffTest
For such a small system, direct eigenvalue computation is used.
The example serves as a good test that the overall stiffness switching framework is behaving as expected.
CUSP
The cusp catastrophe model for the nerve impulse mechanism [Z72]:
Combining with the Van der Pol oscillator gives rise to the CUSP system [HW96]:
Discretization of the diffusion terms using the method of lines is used to obtain a system of ODEs of dimension ![]() .
.
Unlike the Van der Pol system, because of the size of the problem, iterative methods are used for eigenvalue estimation.
Step Size and Order Selection
Jacobian Example
A switch to a stiff method occurs near 0.00113425 and the first test for nonstiffness occurs at the next step ![]() .
.
Norm bounds are quite sharp in this example.
Korteweg–deVries
The Korteweg–deVries partial differential equation is a mathematical model of waves on shallow water surfaces:
We consider boundary conditions
Discretization using the method of lines is used to form a system of 192 ODEs.
Step Sizes

The extrapolation methods never switch back to a nonstiff solver once the stiff solver is chosen at the beginning of the integration.
Therefore this is a form of worst case example for the nonstiff detection.
Despite this, the cost of using subspace iteration is only a few percent of the total integration time.
Jacobian Example
Norm bounds overestimate slightly, but more importantly they give no indication of the relative size of real and imaginary parts.
Option Summary
StiffnessTest
option name | default value | |
| "MaxRepetitions" | {3,5} | specify the maximum number of successive and total times that the stiffness test (6) is allowed to fail |
| "SafetyFactor" | specify the safety factor to use in the right-hand side of the stiffness test (7) |
Options of the method option "StiffnessTest".
