Regression with Uncertainty
Regression with Uncertainty
This section demonstrates using mixture density networks for modeling uncertainty in a regression problem. Such networks model the posterior distribution 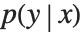 by taking as input the x value and producing as output the parameters of a mixture distribution that approximates
by taking as input the x value and producing as output the parameters of a mixture distribution that approximates 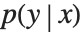 .
.
The following code creates synthetic training data in the form of corresponding x and y values. The data does not represent an ordinary function 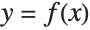 , because for each x value there can be several y values. In addition, the data contains a fair amount of noise:
, because for each x value there can be several y values. In addition, the data contains a fair amount of noise:
An ordinary regression network predicts a single y value when given an input value x (where x and y can be scalars, vectors, matrices, etc.). The basic idea of a density network is to compute a distribution of y values. The network learns the parameters of this distribution as a function of x. A mixture density network learns a mixture of simple distributions. For this example, we use a mixture of six Gaussians.
Construct a net that takes an input number and uses a multilayer perceptron to produce three separate vectors. Each vector contains six numbers that represent parameters for six separate Gaussian components. Two of these vectors ("mean" and "stddev") represent the mean and standard deviation of the Gaussians. The final vector ("weight") is a probability vector that represents how to mix these six Gaussians to produce a single distribution. Note that we use Exp activation to ensure the standard deviation is positive, and we use SoftmaxLayer to ensure the weights sum to 1:
Next, we construct a larger network that trains this parameter net. The larger network takes actual x and y values from our data distribution and calculates the negative log-likelihood, which is a measure of how likely the data is under the model that our parameter net represents. By minimizing this negative log-likelihood, we are effectively maximizing the likelihood of the actual data, which is a common technique to train a probabilistic model.
The training net computes the likelihood of a single y value under the six Gaussians produced by the parameter net. To combine these separate likelihoods into a single likelihood for the mixture of Gaussians, we perform a weighted sum using the weights vector. Lastly, we take the negative of the log.
Construct the training network, using a ThreadingLayer to calculate the Gaussian likelihood, a DotLayer to take the weighted sum of the likelihood across the six Gaussians, and an ElementwiseLayer to turn this into a negative log-likelihood:
Let us take a look at the loss of a randomly initialized net on a single data point to ensure things are working.
Randomly initialize the net with NetInitialize and apply it to a single input:
We can now train the model, which corresponds to simultaneously maximizing the likelihood of the model producing every single one of the points in our dataset. After training, we will extract the parameter net from inside the trained net. We no longer need the training net, as we will not need to calculate negative log-likelihoods on training data again. The parameter net produces an association of means, standard deviations and weights when given an x value.
Train the net with NetTrain for 3000 rounds. Specify LossFunction"Loss" to ensure that NetTrain directly minimizes the output from the port called "Loss", rather than trying to automatically attach a loss layer:
Use NetExtract to extract the trained parameter net from the final trained net:
For each x value in the original data, take one sample from the posterior distribution  calculated by the model:
calculated by the model:
We have learned a density model, because it is efficient for us to calculate the probability density 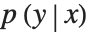 for specific values of x and y. We can delete the layer that computes the negative log of the likelihood from our trained net to produce a net that computes the likelihood instead.
for specific values of x and y. We can delete the layer that computes the negative log of the likelihood from our trained net to produce a net that computes the likelihood instead.
There is a variety of ways we can visualize the behavior of this density model. The simplest is to sample the likelihood at a dense grid of x and y values to produce a density plot. We can also visualize the individual components and how their means and weight values vary as a function of x.
Use CoordinateBoundsArray to create a grid of {x,y} pairs and then flatten these into separate lists of x and y values:
Use the likelihood net to efficiently evaluate the probabilities for these values in a single batch and then unflatten the probabilities to form a matrix again:
The variables "means" and "stddevs" now contain the parameters of the six Gaussian components for each x position. The mixture weights are contained by "weights":
Plot the individual mixture components as envelopes, where the solid lines are the means of each component and the shaded regions show the range of y values covered by the standard deviations.
Define a function that plots a single component by plotting the lines mean-stddev, mean and mean+stddev, with the appropriate shading between them. Then combine these plots into a single plot:
As you can see, it is common for the standard deviation associated with a given component to become very large when corresponding mixture weight is near zero, as that component does not contribute to the model and hence the loss.
Next, we plot the mixture weights as a function of the x value, where the colors match the components shown in the preceding graph.
Use StackedListPlot to plot the six weight values stacked on top of each other as a function of the x value. At each x value, they sum to one, thanks to the SoftmaxLayer[] in the parameter net:
Lastly, we try to visualize both the means of the mixture components and their mixture weights simultaneously. We make the line associated with the component fade out as its mixture weight decreases. Comparing this to the original dataset, it is easier to see how the dominant mixture components at each x value reflect the clustering of the y values in the original dataset at that x value.
Use the ColorFunction option to allow each ListLinePlot to fade out the corresponding mean line, looking up the fade amount in an interpolation function based on the list of weights: