Symmetrized Arrays

Representation of Arrays with SymmetryAntisymmetric Arrays
Construction of Symmetrized Arrays
Symmetry plays a key role in the treatment of high-rank tensors. Most high-rank tensors of importance in physics and mathematics have symmetry, from the symmetric inertia tensors to the rank-4 stiffness and curvature tensors. Many of them have transposition symmetries, in some cases rather complicated. The Wolfram System implements a complete language for permutation symmetries of tensors of any rank or dimensions, and provides a specialized type of array that stores only the independent components with respect to symmetry. This frequently results in a substantial gain in storage space, though usually at the expense of slower manipulations, because more complex algorithms are required. See "Tensor Symmetries" for a description of the language of symmetries.
Representation of Arrays with Symmetry
SymmetrizedArray
construct an array storing only symmetry independent components
SymmetrizedArrayRules
list of rules of independent components of a symmetrized array
SymmetrizedReplacePart
replace independent components in a symmetrized array
Symmetrized arrays.
This is an array with symmetry:
That means that the array stays invariant under all permutations of its slots:
It can be stored a simpler way, which better reflects the fact that some elements are repeated several times:
The new representation contains the dimensions, the list of nonzero independent components, and the symmetry:
Its normal form coincides with the original array:
These are rules for the independent components of the array. The default rule at the end represents the fact that independent components not given here are taken to have value 0:
Symmetrized arrays offer a compact way to store some arrays with much symmetry. In particular, antisymmetry maximizes this gain. In the most extreme nonzero case, a fully antisymmetric rank-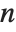 array in dimension 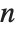has one independent component. Its sparse representation contains 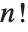nonzero elements, and its normal form has 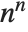entries. On the other hand, manipulation of symmetrized arrays is usually slower because it requires more complex algorithms.
LeviCivitaTensor offers a sparse representation by default:
LeviCivitaTensor offers a symmetrized and normal representation:
Compare sizes of the different representations:
There are other highly symmetric arrays in the Wolfram System.
SymmetrizedArray objects are treated as atomic. Their information can be accessed using functions.
A symmetrized array is atomic:
The information about the array can be obtained as follows:
Extract components of the array, irrespectively of whether they are independent or not:
Extract subarrays, keeping their symmetry if possible:
Individual elements can be changed. Note that the given rule is transformed into its corresponding independent component rule:
Construction of Symmetrized Arrays
It has been shown that SymmetrizedArray can be used to rewrite a normal array with symmetry in a more efficient form. Following SparseArray, SymmetrizedArray can also construct the same efficient representation from a list of rules and a symmetry specification.
SymmetrizedArray form of an antisymmetric matrix:
These are its independent components:
Reconstruct the array from these rules and the symmetry:
If the symmetry is not provided, then the identity symmetry is assumed. The result is effectively equivalent to using SparseArray with the same rules:
Rules that are incompatible with the symmetry are discarded:
General patterns in rules can be used in the first argument of SymmetrizedArray. These rules are meant to be rules for the independent components only, as given by SymmetrizedIndependentComponents, and not for all positions of the array, as SparseArray would do. In particular, this is useful to generate symmetrized arrays with random entries.
A random rank-3 antisymmetric array in dimension 4:
Use indexed expression as components of the array:
An alternative way to construct symmetrized arrays is by actual symmetrization of other arrays, using the function Symmetrize.
Symmetrize a general matrix:
Symmetrized with other symmetries:
Antisymmetric Arrays
The antisymmetric tensors play a fundamental role in exterior algebra. The Wolfram System provides the basic operations of the wedge product of antisymmetric tensors and Hodge duality.
Take two antisymmetric arrays in dimension 5:
Their wedge product is the antisymmetrized tensor product, except for a multiplicative factor given by the multinomial of the ranks:
When the total rank exceeds the dimension, the result vanishes:
The SymmetrizedArray representation allows working with high dimensions; that would not be possible otherwise with normal or sparse representations:
The result is more conveniently represented giving its Hodge dual: