BSplineFunction

BSplineFunction[{pt1,pt2,…}]

represents a B-spline function for a curve defined by the control points pti.

BSplineFunction[array]

represents a B-spline function for a surface or high-dimensional manifold.

Details and Options

  • BSplineFunction is also known as basis spline, nonuniform rational B-spline (NURBS).
  • BSplineFunction[…][u] gives the point on a B-spline curve corresponding to parameter u.
  • BSplineFunction[…][u,v,…] gives the point on a general B-spline manifold corresponding to the parameters u, v, ….
  • The embedding dimension for the curve represented by BSplineFunction[{pt1,pt2,…}] is given by the length of the lists pti.
  • BSplineFunction[array] can handle arrays of any depth, representing manifolds of any dimension.
  • The dimension of the manifold represented by BSplineFunction[array] is given by ArrayDepth[array]-1. The lengths of the lists that occur at the lowest level in the array define the embedding dimension.
  • BSplineFunction[array,d] creates a B-spline function of d variables.
  • The parameters u, v, … by default run from 0 to 1 over the domain of the curve or other manifold.
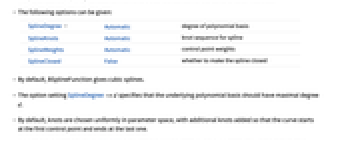
  • The following options can be given:
  • SplineDegree Automaticdegree of polynomial basis
    SplineKnotsAutomaticknot sequence for spline
    SplineWeightsAutomaticcontrol point weights
    SplineClosedFalsewhether to make the spline closed
  • By default, BSplineFunction gives cubic splines.
  • The option setting SplineDegree->d specifies that the underlying polynomial basis should have maximal degree d.
  • By default, knots are chosen uniformly in parameter space, with additional knots added so that the curve starts at the first control point and ends at the last one.
  • With an explicit setting for SplineKnots, the degree of the polynomial basis is determined from the number of knots specified and the number of control points.
  • With the default setting SplineWeights->Automatic, all control points are chosen to have equal weights, corresponding to a polynomial B-spline function.
  • With the setting SplineClosed->{c1,c2,…}, the boundaries are connected in directions i for which ci is True.

Examples

open allclose all

Basic Examples  (2)

Construct a B-spline curve using a list of control points:

Apply the function to find a point on the curve:

Plot the B-spline curve with the control points:

Construct a B-spline surface closed in the u-direction:

Show the surface with the control points:

Scope  (4)

Create a vector-valued function of dimension 2:

Create a vector-valued function of dimension 3:

Generate a two-variable function:

Generate a three-variable function:

Generalizations & Extensions  (1)

SparseArray can be used with BSplineFunction:

Options  (2)

SplineDegree  (2)

Make line segments:

Make a quadratic B-spline curve:

Degrees can be specified in each parametric direction separately:

Wolfram Research (2008), BSplineFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/BSplineFunction.html.

Text

Wolfram Research (2008), BSplineFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/BSplineFunction.html.

CMS

Wolfram Language. 2008. "BSplineFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BSplineFunction.html.

APA

Wolfram Language. (2008). BSplineFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BSplineFunction.html

BibTeX

@misc{reference.wolfram_2024_bsplinefunction, author="Wolfram Research", title="{BSplineFunction}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/BSplineFunction.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_bsplinefunction, organization={Wolfram Research}, title={BSplineFunction}, year={2008}, url={https://reference.wolfram.com/language/ref/BSplineFunction.html}, note=[Accessed: 21-November-2024 ]}