 |
BUILT-IN MATHEMATICA SYMBOL
BlomqvistBetaTest
BlomqvistBetaTest[v1, v2]
tests whether the vectors 
and 
are independent.
BlomqvistBetaTest[m1, m2]
tests whether the matrices 
and 
are independent.
BlomqvistBetaTest[..., "property"]
returns the value of 
.
Details and Options
- BlomqvistBetaTest performs a hypothesis test on
and 
with null hypothesis 
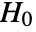that the vectors are independent, and alternative hypothesis 
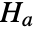that they are not. - By default a probability value or
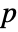-value is returned. - A small
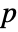-value suggests that it is unlikely that 
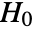is true. - The arguments
and 
can be any real-valued vectors or matrices of equal length. - BlomqvistBetaTest is based on Blomqvist's medial correlation coefficient
computed by BlomqvistBeta[v1, v2]. - For testing matrices the test statistic is based on inner standardized spatial signs and asymptotically follows a ChiSquareDistribution[r*s] where r and s are the dimension of
and 
, respectively. The test statistic is invariant under affine transformations. - BlomqvistBetaTest[v1, v2, "HypothesisTestData"] returns a HypothesisTestData object htd that can be used to extract additional test results and properties using the form htd["property"].
- BlomqvistBetaTest[v1, v2, "property"] can be used to directly give the value of
. - Properties related to the reporting of test results include:
-
"DegreesOfFreedom" the degrees of freedom used in the test "PValue" the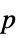 
-value of the test"PValueTable" formatted table containing the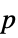 
-value"ShortTestConclusion" a short description of the conclusion of the test "TestConclusion" a description of the conclusion of the test "TestData" a list containing the test statistic and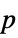 
-value"TestDataTable" formatted table of the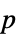 
-value and test statistic"TestStatistic" the test statistic "TestStatisticTable" formatted table containing the test statistic - The following options can be used:
-
AlternativeHypothesis "Unequal" the inequality for the alternative hypothesis MaxIterations Automatic max iterations for multivariate test Method Automatic the method to use for computing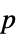 
-valuesSignificanceLevel 0.05 cutoff for diagnostics and reporting - For tests of independence, a cutoff
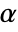is chosen such that 
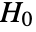is rejected only if 
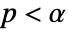. The value of 
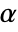used for the 
and 
properties is controlled by the SignificanceLevel option. By default 
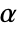is set to 
.
New in 9
