FactorialMoment[data,r]
gives the order r![]() factorial moment
factorial moment ![]() of data.
of data.
FactorialMoment[data,{r1,…,rm}]
gives the order {r1,…,rm} multivariate factorial moment ![]() of data.
of data.
FactorialMoment[dist,…]
gives the factorial moment of the distribution dist.
represents the order r![]() formal factorial moment.
formal factorial moment.


FactorialMoment
FactorialMoment[data,r]
gives the order r![]() factorial moment
factorial moment ![]() of data.
of data.
FactorialMoment[data,{r1,…,rm}]
gives the order {r1,…,rm} multivariate factorial moment ![]() of data.
of data.
FactorialMoment[dist,…]
gives the factorial moment of the distribution dist.
represents the order r![]() formal factorial moment.
formal factorial moment.
Details


- Factorial moments are defined using FactorialPower[x,r] given by
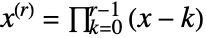 .
. - For scalar order r and data being an array
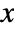 :
: -
![x in TemplateBox[{Vectors, paclet:ref/Vectors}, RefLink, BaseStyle -> {3ColumnTableMod}][n] x in TemplateBox[{Vectors, paclet:ref/Vectors}, RefLink, BaseStyle -> {3ColumnTableMod}][n]](Files/FactorialMoment.en/8.png)
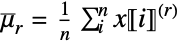
sum of r 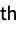 factorial powers »
factorial powers »![x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}] x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}]](Files/FactorialMoment.en/11.png)
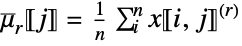
columnwise sum of r 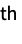 factorial powers »
factorial powers »![x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}] x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}]](Files/FactorialMoment.en/14.png)
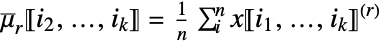
columnwise sum of r 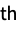 factorial powers »
factorial powers » - FactorialMoment[x,r] is equivalent to ArrayReduce[FactorialMoment[#,r]&,x,1].
- For vector order {r1,…,rm} and data being array
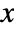 :
: -
![x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}] x in TemplateBox[{Matrices, paclet:ref/Matrices}, RefLink, BaseStyle -> {3ColumnTableMod}][{n,m}]](Files/FactorialMoment.en/18.png)
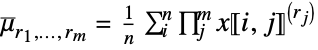
sum the rj 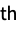 factorial power in the j
factorial power in the j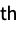 column
column![x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}] x in TemplateBox[{Arrays, paclet:ref/Arrays}, RefLink, BaseStyle -> {3ColumnTableMod}][{n_(1),...,n_(k)}]](Files/FactorialMoment.en/22.png)
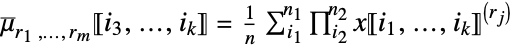
sum the rj 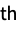 factorial power in the j
factorial power in the j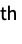 column »
column » - FactorialMoment[x,{r1,…,rm}] is equivalent to ArrayReduce[FactorialMoment[#,{r1,…,rm}]&,x,{{1},{2}}].
- FactorialMoment handles both numerical and symbolic data.
- The data can have the following additional forms and interpretations:
-
Association the values (the keys are ignored) » WeightedData weighted mean, based on the underlying EmpiricalDistribution » EventData based on the underlying SurvivalDistribution » TimeSeries, TemporalData, … vector or array of values (the time stamps ignored) » Image,Image3D RGB channel's values or grayscale intensity value » Audio amplitude values of all channels » - For a distribution dist, the r
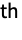 factorial moment is given by Expectation[x(r),xdist]. »
factorial moment is given by Expectation[x(r),xdist]. » - For a multivariate distribution dist, the {r1,…,rm}
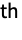 factorial moment is given by Expectation[x1(r1)⋯ xm(rm),{x1,…,xm}dist]. »
factorial moment is given by Expectation[x1(r1)⋯ xm(rm),{x1,…,xm}dist]. » - For a random process proc, the factorial moment function can be computed for slice distribution at time t, SliceDistribution[proc,t], as
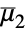 [t]=FactorialMoment[SliceDistribution[proc,t],r]. »
[t]=FactorialMoment[SliceDistribution[proc,t],r]. » - FactorialMoment[r] can be used in such functions as MomentConvert and MomentEvaluate, etc. »
Examples
open all close allBasic Examples (2)
Scope (20)
Basic Uses (5)
Exact input yields exact output:
Approximate input yields approximate output:
Find factorial moments of WeightedData:
Find a factorial moment of EventData:
Find a factorial moment of TimeSeries:
Array Data (4)
For a matrix, FactorialMoment gives columnwise moments:
For an array, FactorialMoment gives columnwise moments at the first level:
Multivariate FactorialMoment for an array:
When the input is an Association, FactorialMoment works on its values:
SparseArray data can be used just like dense arrays:
Image and Audio Data (2)
Channelwise factorial moment of an RGB image:
Factorial moment intensity value of a grayscale image:
On audio objects, FactorialMoment works channelwise:
Distribution and Process Moments (5)
Scalar factorial moment for univariate distributions:
Scalar factorial moment for multivariate distributions:
Joint factorial moment for multivariate distributions:
Compute a factorial moment for a symbolic order r:
A factorial moment may only evaluate for specific orders:
A factorial moment may only evaluate numerically:
Factorial moments for derived distributions:
Factorial moment function for a random process:
Find a factorial moment of TemporalData at some time t=0.5:
Find the corresponding factorial moment function together with all the simulations:
Formal Moments (4)
TraditionalForm formatting for formal moments:
Convert combinations of formal moments to an expression involving FactorialMoment:
Evaluate an expression involving formal moments ![]() for a distribution:
for a distribution:
Find a sample estimator for an expression involving FactorialMoment:
Applications (4)
Estimate parameters of a distribution using the method of factorial moments:
Compare data and the estimated parametric distribution:
Reconstruct probability mass function from the sequence of factorial moments:
Find the factorial moment-generating function (FMGF):
Use equivalence of the FMGF and the probability generating function:
Verify that factorial moments of the found distribution match the originals:
Compute a moving factorial moment for some data:
Compute factorial moments for slices of a collection of paths of a random process:
Properties & Relations (5)
Factorial moment ![]() is equivalent to an expectation of FactorialPower:
is equivalent to an expectation of FactorialPower:
First factorial moment is equivalent to Mean:
FactorialMoment can be computed from Moment through ![]() :
:
MomentConvert produces the same result:
Moment can be computed from FactorialMoment through ![]() :
:
MomentConvert produces the same result:
The multivariate factorial moment of an array of depth ![]() has depth
has depth ![]() :
:
Neat Examples (1)
The distribution of FactorialMoment estimates for 30, 100, and 300 samples:
Text
Wolfram Research (2010), FactorialMoment, Wolfram Language function, https://reference.wolfram.com/language/ref/FactorialMoment.html (updated 2024).
CMS
Wolfram Language. 2010. "FactorialMoment." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/FactorialMoment.html.
APA
Wolfram Language. (2010). FactorialMoment. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FactorialMoment.html
BibTeX
@misc{reference.wolfram_2025_factorialmoment, author="Wolfram Research", title="{FactorialMoment}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/FactorialMoment.html}", note=[Accessed: 11-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_factorialmoment, organization={Wolfram Research}, title={FactorialMoment}, year={2024}, url={https://reference.wolfram.com/language/ref/FactorialMoment.html}, note=[Accessed: 11-March-2026]}