FindIntegerNullVector[{x1,x2,…,xn}]
finds a list of integers ![]() such that
such that ![]() .
.
FindIntegerNullVector[{x1,x2,…,xn},d]
finds a list of integers ![]() with
with ![]() such that
such that ![]() .
.


FindIntegerNullVector
FindIntegerNullVector[{x1,x2,…,xn}]
finds a list of integers ![]() such that
such that ![]() .
.
FindIntegerNullVector[{x1,x2,…,xn},d]
finds a list of integers ![]() with
with ![]() such that
such that ![]() .
.
Details and Options

- FindIntegerNullVector is also known as PSLQ or number identification.
- Not all ai are zero. The numbers xi can be real or complex. For complex numbers xi the numbers ai are Gaussian integers.
- In FindIntegerNullVector[{x1,x2,…},d] no integer null vector may exist with the given norm bound. The input is then returned unevaluated.
- The following options can be given:
-
WorkingPrecision Automatic precision to use in internal computation ZeroTest Automatic method to test whether a number is zero - The setting ZeroTest->Automatic automatically determines the method to test the integer relation
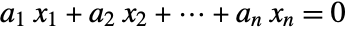 .
. - For inexact numbers xi, the relation found holds up to the precision of the input. For exact numbers xi, the relation found is validated using PossibleZeroQ.
- For inexact numbers xi and WorkingPrecision->Automatic the precision is taken to be the precision of the input.
- For exact numbers xi and WorkingPrecision->Automatic the precision is taken to start with MachinePrecision and use up to $MaxExtraPrecision extra precision when searching for an integer null vector when no norm bound d is specified. In the case of a norm bound d, enough precision is used to either find a null vector or prove that none exist.
Examples
open all close allBasic Examples (3)
Scope (6)
This finds an integer null vector for a vector of exact real numbers:
This proves that there is no null vector with norm less than or equal to 8:
For a bound close to the norm of a null vector you may not get proof that no null vector exists:

The returned null vector does not satisfy the norm bound:
FindIntegerNullVector cannot prove that numbers are linearly independent over the integers:
It can prove that there is no integer null vector with norm less than or equal to a given bound:
For inexact input, the relation is true up to the precision of the input:
No null vector exists for the given norm bound:
Here no null vector is found, but nonexistence of a null vector is proven only for a smaller norm bound:

This finds a null vector for a 20-digit approximation of ![]() :
:
The result is not a null vector for the exact vector ![]() :
:
A null vector found for a higher-precision approximation of ![]() is also a null vector for
is also a null vector for ![]() :
:
This gives a Gaussian integer null vector for a vector of exact complex numbers:
This finds a Gaussian integer null vector for a vector of approximate complex numbers:
Options (2)
WorkingPrecision (1)
By default, precision of at most $MachinePrecision+$MaxExtraPrecision digits is used:
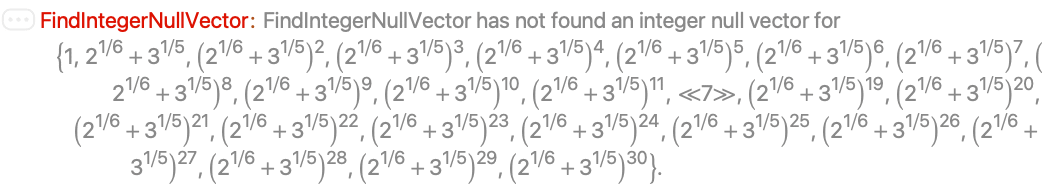
Using a higher WorkingPrecision allows you to find a null vector:
ZeroTest (1)
By default, PossibleZeroQ with Method->"ExactAlgebraics" is used to prove relations:
Applications (3)
Properties & Relations (3)
FindIntegerNullVector returns an integer null vector for the given vector:
An integer null vector is a nontrivial integer solution of a homogeneous linear equation:
Use FindInstance to find solutions of equations:
Find coefficients of the minimal polynomial of an algebraic number using its approximation:
Use RootApproximant to find an algebraic number using its approximation:
Possible Issues (2)
The precision of an approximation may not be sufficient to find a relation between numbers:
Using a higher-precision approximation, you get a true relation:
Numeric zero testing used for nonalgebraic numbers may allow results that are not null vectors:
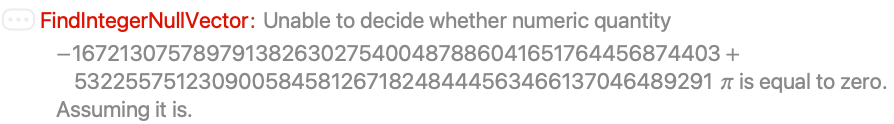
This gives the precision used in zero testing when no symbolic zero-testing method applies:
With a higher zero-testing precision, FindIntegerNullVector correctly rejects the vector:
Related Guides
History
Text
Wolfram Research (2010), FindIntegerNullVector, Wolfram Language function, https://reference.wolfram.com/language/ref/FindIntegerNullVector.html.
CMS
Wolfram Language. 2010. "FindIntegerNullVector." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FindIntegerNullVector.html.
APA
Wolfram Language. (2010). FindIntegerNullVector. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindIntegerNullVector.html
BibTeX
@misc{reference.wolfram_2025_findintegernullvector, author="Wolfram Research", title="{FindIntegerNullVector}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/FindIntegerNullVector.html}", note=[Accessed: 13-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_findintegernullvector, organization={Wolfram Research}, title={FindIntegerNullVector}, year={2010}, url={https://reference.wolfram.com/language/ref/FindIntegerNullVector.html}, note=[Accessed: 13-December-2025]}