FindRoot
FindRoot[f,{x,x0}]
searches for a numerical root of f, starting from the point x=x0.
FindRoot[lhs==rhs,{x,x0}]
searches for a numerical solution to the equation lhs==rhs.
FindRoot[{f1,f2,…},{{x,x0},{y,y0},…}]
searches for a simultaneous numerical root of all the fi.
FindRoot[{eqn1,eqn2,…},{{x,x0},{y,y0},…}]
searches for a numerical solution to the simultaneous equations eqni.
Details and Options

- If the starting point for a variable is given as a list, the values of the variable are taken to be lists with the same dimensions.
- FindRoot returns a list of replacements for x, y, … , in the same form as obtained from Solve.
- FindRoot first localizes the values of all variables, then evaluates f with the variables being symbolic, and then repeatedly evaluates the result numerically.
- FindRoot has attribute HoldAll, and effectively uses Block to localize variables.
- FindRoot[lhs==rhs,{x,x0,x1}] searches for a solution using x0 and x1 as the first two values of x, avoiding the use of derivatives.
- FindRoot[lhs==rhs,{x,xstart,xmin,xmax}] searches for a solution, stopping the search if x ever gets outside the range xmin to xmax.
- If you specify only one starting value of x, FindRoot searches for a solution using Newton methods. If you specify two starting values, FindRoot uses a variant of the secant method.
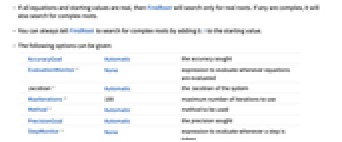
- If all equations and starting values are real, then FindRoot will search only for real roots. If any are complex, it will also search for complex roots.
- You can always tell FindRoot to search for complex roots by adding 0.I to the starting value.
- The following options can be given:
-
AccuracyGoal Automatic the accuracy sought EvaluationMonitor None expression to evaluate whenever equations are evaluated Jacobian Automatic the Jacobian of the system MaxIterations 100 maximum number of iterations to use ![TemplateBox[{Method, paclet:ref/Method}, RefLink, BaseStyle -> {3ColumnTableMod}] TemplateBox[{Method, paclet:ref/Method}, RefLink, BaseStyle -> {3ColumnTableMod}]](Files/FindRoot.en/1.png)
Automatic method to be used PrecisionGoal Automatic the precision sought StepMonitor None expression to evaluate whenever a step is taken WorkingPrecision MachinePrecision the precision to use in internal computations - The default settings for AccuracyGoal and PrecisionGoal are WorkingPrecision/2.
- The setting for AccuracyGoal specifies the number of digits of accuracy to seek in both the value of the position of the root, and the value of the function at the root.
- The setting for PrecisionGoal specifies the number of digits of precision to seek in the value of the position of the root.
- FindRoot continues until either of the goals specified by AccuracyGoal or PrecisionGoal is achieved.
- If FindRoot does not succeed in finding a solution to the accuracy you specify within MaxIterations steps, it returns the most recent approximation to a solution that it found. You can then apply FindRoot again, with this approximation as a starting point.
Examples
open allclose allBasic Examples (3)
Scope (4)
Generalizations & Extensions (1)
Options (9)
AccuracyGoal and PrecisionGoal (1)
EvaluationMonitor (1)
EvaluationMonitor can be used to keep track of function evaluations used:
Jacobian (1)
Specify the Jacobian for a "black-box" function:
Without a specified Jacobian, extra evaluations are used to compute finite differences:
If you just know the sparse form, specifying the sparse pattern template saves evaluations:
Inspect the number of Jacobian evaluations needed by different methods:
MaxIterations (1)
Method (2)
Method options are also explained in Unconstrained Optimization.
Find a root for![]() using different methods:
using different methods:
Define a function that monitors the steps and evaluations used by FindRoot:
The default (Newton's) method:
Brent's root-bracketing method requiring two initial conditions bracketing the root:
StepMonitor (1)
Applications (3)
Computing Inverse Functions (1)
For an isomorphism ![]() , the inverse
, the inverse ![]() is the root of
is the root of ![]() :
:
An approximate inverse for the exponential function:
It is very close to the built-in Log function:
Solving Boundary Value Problems (2)
Properties & Relations (2)
For a polynomial system of equations, NSolve finds all solutions and FindRoot finds one:
FindRoot will find a single solution using an iterative method:
NSolve will find all solutions using a direct method:
For equations involving parameters or exact solutions use Solve, Reduce, or FindInstance:
Solve will return some solutions:
Reduce will enumerate all solutions:
FindInstance will find particular instances:
Text
Wolfram Research (1988), FindRoot, Wolfram Language function, https://reference.wolfram.com/language/ref/FindRoot.html (updated 2003).
CMS
Wolfram Language. 1988. "FindRoot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2003. https://reference.wolfram.com/language/ref/FindRoot.html.
APA
Wolfram Language. (1988). FindRoot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindRoot.html