Some Notes on Internal Implementation
Some Notes on Internal Implementation
| Introduction | Numerical and Related Functions |
| Data Structures and Memory Management | Algebra and Calculus |
| Basic System Features | Output and Interfacing |
General issues about the internal implementation of the Wolfram Language are discussed in "The Internals of the Wolfram System". Given here are brief notes on particular features.
It should be emphasized that these notes give only a rough indication of basic methods and algorithms used. The actual implementation usually involves many substantial additional elements.
Thus, for example, the notes simply say that DSolve solves second-order linear differential equations using the Kovacic algorithm. But the internal code that achieves this is over 60 pages long, includes a number of other algorithms, and involves a great many subtleties.
A Wolfram Language expression internally consists of a contiguous array of pointers, the first to the head, and the rest to its successive elements.
Each expression contains a special form of hash code that is used both in pattern matching and evaluation.
For every symbol there is a central symbolic table entry that stores all information about the symbol.
Most raw objects such as strings and numbers are allocated separately; however, unique copies are maintained of small integers and of certain approximate numbers generated in computations.
Every piece of memory used by the Wolfram Language maintains a count of how many times it is referenced. Memory is automatically freed when this count reaches zero.
The contiguous storage of elements in expressions reduces memory fragmentation and swapping. However, it can lead to the copying of a complete array of pointers when a single element in a long expression is modified. Many optimizations based on reference counts and pre-allocation are used to avoid such copying.
When appropriate, large lists and nested lists of numbers are automatically stored as packed arrays of machine-sized integers or real numbers. The Wolfram Language compiler is automatically used to compile complicated functions that will be repeatedly applied to such packed arrays. The Wolfram Symbolic Transfer Protocol (WSTP), DumpSave, and various Import and Export formats make external use of packed arrays.
The Wolfram Language is fundamentally an interpreter that scans through expressions calling internal code pointed to by the symbol table entries of heads that it encounters.
Any transformation rule—whether given as x->y or in a definition—is automatically compiled into a form that allows for rapid pattern matching. Many different types of patterns are distinguished and are handled by special code.
A form of hashing that takes account of blanks and other features of patterns is used in pattern matching.
When a large number of definitions is given for a particular symbol, a hash table is automatically built using a version of Dispatch so that appropriate rules can quickly be found.
Number Representation and Numerical Evaluation
- Large integers and high-precision approximate numbers are stored as arrays of base
 or
or  digits, depending on the lengths of machine integers.
digits, depending on the lengths of machine integers.
- IntegerDigits, RealDigits, and related base conversion functions use recursive divide-and-conquer algorithms. Similar algorithms are used for number input and output.
- N uses an adaptive procedure to increase its internal working precision in order to achieve whatever overall precision is requested.
- Floor, Ceiling, and related functions use an adaptive procedure similar to N to generate exact results from exact input.
Basic Arithmetic
- Multiplication of large integers and high-precision approximate numbers is done using interleaved schoolbook, Karatsuba, three-way Toom–Cook, and number-theoretic transform algorithms.
- Significance arithmetic is used by default for all arithmetic with approximate numbers not equal to machine precision.
Pseudorandom Numbers
- The default pseudorandom number generator for functions like RandomReal and RandomInteger uses a cellular automaton-based algorithm.
Number Theoretic Functions
- GCD interleaves the HGCD algorithm, the Jebelean–Sorenson–Weber accelerated GCD algorithm, and a combination of Euclid's algorithm and an algorithm based on iterative removal of powers of 2.
- PrimeQ first tests for divisibility using small primes, then uses the Miller–Rabin strong pseudoprime test base 2 and base 3, and then uses a Lucas test.
- The Primality Proving Package contains a much slower algorithm that has been proved correct for all
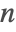 . It can return an explicit certificate of primality.
. It can return an explicit certificate of primality.
- FactorInteger switches between trial division, Pollard
 , Pollard rho, elliptic curve, and quadratic sieve algorithms.
, Pollard rho, elliptic curve, and quadratic sieve algorithms.
- Prime and PrimePi use sparse caching and sieving. For large
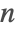 , the Lagarias–Miller–Odlyzko algorithm for PrimePi is used, based on asymptotic estimates of the density of primes, and is inverted to give Prime.
, the Lagarias–Miller–Odlyzko algorithm for PrimePi is used, based on asymptotic estimates of the density of primes, and is inverted to give Prime.
- LatticeReduce uses Storjohann's variant of the Lenstra–Lenstra–Lovasz lattice reduction algorithm.
- To find a requested number of terms, ContinuedFraction uses a modification of Lehmer's indirect method, with a self-restarting divide-and-conquer algorithm to reduce the numerical precision required at each step.
- ContinuedFraction uses recurrence relations to find periodic continued fractions for quadratic irrationals.
- FromContinuedFraction uses iterated matrix multiplication optimized by a divide-and-conquer method.
Combinatorial Functions
- Binomial and related functions use a divide-and-conquer algorithm to balance the number of digits in subproducts.
- Fibonacci[n] uses an iterative method based on the binary digit sequence of
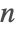 .
.
- PartitionsP[n] uses Euler's pentagonal formula for small
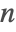 and the non-recursive Hardy–Ramanujan–Rademacher method for larger
and the non-recursive Hardy–Ramanujan–Rademacher method for larger 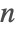 .
.
- ClebschGordan and related functions use generalized hypergeometric series.
- Bernoulli numbers are computed using recurrence equations or the Fillebrown algorithm depending on the number's index.
Elementary Transcendental Functions
- Exponential and trigonometric functions use Taylor series, stable recursion by argument doubling, and functional relations.
Mathematical Constants
- Pi is computed using the Chudnovsky formula.
- E is computed from its series expansion.
- EulerGamma uses the Brent–McMillan algorithm.
- Catalan is computed using a generalized hypergeometric sum.
Special Functions
- For machine precision most special functions use Wolfram Language-derived rational minimax approximations. The notes that follow apply mainly to arbitrary precision.
- Orthogonal polynomials use stable recursion formulas for polynomial cases and hypergeometric functions in general.
- Gamma uses recursion, functional equations, and the Binet asymptotic formula.
- PolyGamma uses Euler–Maclaurin summation, functional equations, and recursion.
- PolyLog uses Euler–Maclaurin summation, expansions in terms of incomplete gamma functions, numerical quadrature, and a functional equation of the Hurwitz zeta function.
- Zeta and related functions use Euler–Maclaurin summation and functional equations. Near the critical strip they also use the Riemann–Siegel formula.
- StieltjesGamma uses Keiper's algorithm based on numerical quadrature of an integral representation of the zeta function and alternating series summation using Bernoulli numbers.
- Bessel functions use series and asymptotic expansions. For integer orders, some also use stable forward recursion.
- The hypergeometric functions use functional equations, stable recurrence relations, series expansions, asymptotic series, and Padé approximants. Methods from NSum and NIntegrate are also sometimes used.
- ProductLog uses high-order Newton's method starting from rational approximations and asymptotic expansions.
- Elliptic theta functions use series summation with recursive evaluation of series terms and modular transformations.
- Mathieu functions use Fourier series. The Mathieu characteristic functions use generalizations of Blanch's Newton method.
Numerical Integration
- NIntegrate uses symbolic preprocessing to resolve function symmetries, expand piecewise functions into cases, and decompose regions specified by inequalities into cells.
- With Method->Automatic, NIntegrate uses "GaussKronrod" in one dimension, and "MultiDimensional" otherwise.
- If an explicit setting for MaxPoints is given, NIntegrate by default uses Method->"QuasiMonteCarlo".
- "GaussKronrod": adaptive Gaussian quadrature with error estimation based on evaluation at Kronrod points.
- "Oscillatory": transformation to handle certain integrals containing trigonometric and Bessel functions.
Numerical Sums and Products
- If the ratio test does not give 1, the Wynn epsilon algorithm is applied to a sequence of partial sums or products.
- Otherwise Euler–Maclaurin summation is used with Integrate or NIntegrate.
Numerical Differential Equations
- For ordinary differential equations, NDSolve by default uses an LSODA approach, switching between a non-stiff Adams method and a stiff Gear backward differentiation formula method.
- The code for NDSolve and related functions is about 1400 pages long.
Approximate Equation Solving and Optimization
- For sparse linear systems, Solve and NSolve use several efficient numerical methods, mostly based on Gauss factoring with Markowitz products (approximately 250 pages of code).
- For systems of algebraic equations, NSolve computes a numerical Gröbner basis using an efficient monomial ordering, then uses eigensystem methods to extract numerical roots.
- FindRoot uses a damped Newton's method, the secant method, and Brent's method.
- With Method->Automatic and two starting values, FindMinimum uses Brent's principal axis method. With one starting value for each variable, FindMinimum uses BFGS quasi-Newton methods, with a limited memory variant for large systems.
- If the function to be minimized is a sum of squares, FindMinimum uses the Levenberg–Marquardt method (Method->"LevenbergMarquardt").
- With constraints, FindMinimum uses interior point methods.
- LinearProgramming uses simplex and revised simplex methods, and with Method->"InteriorPoint" uses primal-dual interior point methods.
- For linear cases, NMinimize and NMaximize use the same methods as LinearProgramming. For nonlinear cases, they use Nelder–Mead methods, supplemented by differential evolution, especially when integer variables are present.
- LeastSquares uses LAPACK's least-squares functions.
Data Manipulation
- Fourier uses the FFT algorithm with decomposition of the length into prime factors. When the prime factors are large, fast convolution methods are used to maintain
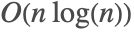 asymptotic complexity.
asymptotic complexity.
- For real input, Fourier uses a real transform method.
- ListConvolve and ListCorrelate use FFT algorithms when possible. For exact integer inputs, binary segmentation is used to reduce the problem to large integer multiplication.
- InterpolatingFunction uses divided differences to construct Lagrange or Hermite interpolating polynomials.
- Fit works using singular value decomposition. FindFit uses the same method for the linear least-squares case, the Levenberg–Marquardt method for nonlinear least-squares, and general FindMinimum methods for other norms.
- CellularAutomaton often uses bit-packed parallel operations with bit slicing. For elementary rules, parallel operations are implemented using optimal Boolean functions, while for many totalistic rules, just-in-time-compiled bit-packed tables are used. In two dimensions, for two-color quiescent rules that operate on the Moore neighborhood and states with infinite background, sparse bit-packed arrays are used when possible, with only active clusters updated.
Approximate Numerical Linear Algebra
- Machine-precision matrices are typically converted to a special internal representation for processing.
- SparseArray with rules involving patterns uses cylindrical algebraic decomposition to find connected array components. Sparse arrays are stored internally using compressed sparse row formats, generalized for tensors of arbitrary rank.
- LUDecomposition, Inverse, RowReduce, and Det use Gaussian elimination with partial pivoting. LinearSolve uses the same methods, together with adaptive iterative improvement for high-precision numbers.
- For sparse arrays, LinearSolve uses UMFPACK multifrontal direct solver methods and with Method->"Krylov" uses Krylov iterative methods preconditioned by an incomplete LU factorization. For high-precision numbers, it uses adaptive iterative improvement methods. Eigenvalues and Eigenvectors use ARPACK Arnoldi methods.
- SingularValueDecomposition uses the QR algorithm with Givens rotations. PseudoInverse, NullSpace, and MatrixRank are based on SingularValueDecomposition. For sparse arrays, Arnoldi methods are used.
- QRDecomposition uses Householder transformations.
- SchurDecomposition uses QR iteration.
- MatrixExp uses variable-order Padé approximation, evaluating rational matrix functions using Paterson–Stockmeyer methods or Krylov subspace approximations.
Exact Numerical Linear Algebra
- Inverse and LinearSolve use efficient row reduction based on numerical approximation.
- With Modulus->n, modular Gaussian elimination is used.
- Det uses modular methods and row reduction, constructing a result using the Chinese remainder theorem.
- Eigenvalues works by interpolating the characteristic polynomial.
- MatrixExp uses Putzer's method or Jordan decomposition.
Polynomial Manipulation
- For univariate polynomials, Factor uses a variant of the Cantor–Zassenhaus algorithm to factor modulo a prime, then uses Hensel lifting and recombination to build up factors over the integers.
- Factoring over algebraic number fields is done by finding a primitive element over the rationals and then using Trager's algorithm.
- For multivariate polynomials Factor works by substituting appropriate choices of integers for all but one variable, then factoring the resulting univariate polynomials and reconstructing multivariate factors using Wang's algorithm.
- The internal code for Factor exclusive of general polynomial manipulation is about 250 pages long.
- FactorSquareFree works by finding a derivative and then iteratively computing GCDs.
- Resultant uses either explicit subresultant polynomial remainder sequences or modular sequences accompanied by the Chinese remainder theorem.
- Apart uses either a version of the Padé technique or the method of undetermined coefficients.
- PolynomialGCD and Together usually use modular algorithms, including Zippel's sparse modular algorithm, but in some cases use subresultant polynomial remainder sequences.
Symbolic Linear Algebra
- RowReduce, LinearSolve, NullSpace, and MatrixRank are based on Gaussian elimination.
- Inverse uses cofactor expansion and row reduction. Pivots are chosen heuristically by looking for simple expressions.
- Det uses direct cofactor expansion for small matrices and Gaussian elimination for larger ones.
- MatrixExp finds eigenvalues and then uses Putzer's method.
- Zero testing for various functions is done using symbolic transformations and interval-based numerical approximations after random numerical values have been substituted for variables.
Exact Equation Solving and Reduction
- Root objects representing algebraic numbers are usually isolated and manipulated using validated numerical methods. With ExactRootIsolation->True, Root uses for real roots a continued fraction version of an algorithm based on Descartes's rule of signs, and for complex roots the Collins–Krandick algorithm.
- For single polynomial equations, Solve uses explicit formulas up to degree four, attempts to reduce polynomials using Factor and Decompose, and recognizes cyclotomic and other special polynomials.
- For systems of polynomial equations, Solve constructs a Gröbner basis.
- Solve and GroebnerBasis use an efficient version of the Buchberger algorithm.
- For non-polynomial equations, Solve attempts to change variables and add polynomial side conditions.
- The code for Solve and related functions is about 500 pages long.
- For polynomial systems, Reduce uses cylindrical algebraic decomposition for real domains and Gröbner basis methods for complex domains.
- With algebraic functions, Reduce constructs equivalent purely polynomial systems. With transcendental functions, Reduce generates polynomial systems composed with transcendental conditions, then reduces these using functional relations and a database of inverse image information. With piecewise functions, Reduce does symbolic expansion to construct a collection of continuous systems.
- For univariate transcendental equations, Reduce represents solutions as transcendental Root objects. For exp-log function equations over the reals, Reduce uses an exact exp-log root isolation algorithm. For analytic function equations over bounded real or complex domains, Reduce finds roots using validated numerical methods. For elementary functions, both the number and the location of roots are fully validated using interval arithmetic methods. For non-elementary functions, validation of the number of roots depends on correctness of numeric integration and validation of the location of roots depends on correctness of accuracy estimates provided by the Wolfram Language's significance arithmetic.
- CylindricalDecomposition uses the Collins–Hong algorithm with Brown–McCallum projection for well-oriented sets and Hong projection for other sets. CAD construction is done by Strzebonski's genealogy-based method using validated numerics backed up by exact algebraic number computation. For zero-dimensional systems Gröbner basis methods are used.
- GenericCylindricalDecomposition uses a simplified version of the CAD algorithm that uses a simpler projection operator and constructs only cells with rational number sample points.
- For Diophantine systems, Reduce solves linear equations using Hermite normal form, and linear inequalities using Contejean–Devie methods. For univariate polynomial equations, it uses an improved Cucker–Koiran–Smale method, while for bivariate quadratic equations, it uses Hardy–Muskat–Williams methods for ellipses and classical techniques for Pell and other cases. Reduce includes specialized methods for about 25 classes of Diophantine equations, including the Tzanakis–de Weger algorithm for Thue equations.
- With prime moduli, Reduce uses linear algebra for linear equations and Gröbner bases over prime fields for polynomial equations. For composite moduli, it uses Hermite normal form and Gröbner bases over integers.
- Reduce and related functions use about 350 pages of Wolfram Language code and 1400 pages of C code.
Exact Optimization
- For linear cases, Minimize and Maximize use exact linear programming methods. For polynomial cases they use cylindrical algebraic decomposition. For analytic cases in closed and bounded boxes they use methods based on Lagrange multipliers.
- For bounded linear cases with integer variables, Minimize and Maximize use a branch-and-bound method for integer linear programming, with preprocessing done by lattice reduction.
- Piecewise functions are symbolically expanded, with each case being treated as a separate optimization problem.
Simplification
- FullSimplify automatically applies about 40 types of general algebraic transformations, as well as about 400 types of rules for specific mathematical functions.
- Generalized hypergeometric functions are simplified using about 70 pages of Wolfram Language transformation rules. These functions are fundamental to many calculus operations in the Wolfram Language.
- FunctionExpand uses an extension of Gauss's algorithm to expand trigonometric functions with arguments that are rational multiples of
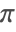 .
.
- Simplify and FullSimplify cache results when appropriate.
- When assumptions specify that variables are real, polynomial constraints are handled by cylindrical algebraic decomposition, while linear constraints are handled by the simplex algorithm or Loos–Weispfenning linear quantifier elimination. For strict polynomial inequalities, Strzebonski's generic CAD algorithm is used.
- For non-algebraic functions, a database of relations is used to determine the domains of function values from the domains of their arguments. Polynomial-oriented algorithms are used whenever the resulting domains correspond to semialgebraic sets.
- For integer functions, several hundred theorems of number theory are used in the form of Wolfram Language rules.
Differentiation and Integration
- For indefinite integrals, an extended version of the Risch algorithm is used whenever both the integrand and integral can be expressed in terms of elementary functions, exponential integral functions, polylogarithms, and other related functions.
- The algorithms in the Wolfram Language cover all of the indefinite integrals in standard reference books such as Gradshteyn–Ryzhik.
- Definite integrals that involve no singularities are mostly done by taking limits of the indefinite integrals.
- Many other definite integrals are done using Marichev–Adamchik Mellin transform methods. The results are often initially expressed in terms of Meijer G functions, which are converted into hypergeometric functions using Slater's theorem and then simplified.
- Integrals over multidimensional regions defined by inequalities are computed by iterative decomposition into disjoint cylindrical or triangular cells.
- Integrate uses about 500 pages of Wolfram Language code and 600 pages of C code.
Differential Equations
- Second-order linear equations with variable coefficients whose solutions can be expressed in terms of elementary functions and their integrals are solved using the Kovacic algorithm.
- Linear equations with rational function coefficients are solved in terms of special functions by using Mellin transforms. Equations with more general coefficients are if possible reduced using variable transformations.
- Systems of linear equations with rational function coefficients whose solutions can be given as rational functions are solved using Abramov–Bronstein elimination algorithms.
- When possible, nonlinear equations are solved by symmetry reduction techniques. For first-order equations many classical techniques are used; for second-order equations and systems integrating factor and Bocharov techniques are used. Abel equations are solved by computing invariants to determine equivalence classes.
- Piecewise equations are typically solved by decomposition into collections of boundary-value problems.
- The algorithms in the Wolfram Language cover almost all of the ordinary differential equations in standard reference books such as Kamke.
- For linear and quasilinear partial differential equations, separation of variables and symmetry reduction are used.
- For first-order nonlinear PDEs, complete integrals are computed by reduction through Legendre, Euler and other transformations.
- For differential-algebraic equations, a method based on isolating singular parts by core nilpotent decomposition is used.
- Factorization methods for higher-order differential equations use techniques due to Bronstein and van Hoeij.
- DSolve uses about 300 pages of Wolfram Language code and 200 pages of C code.
Sums and Products
- Special algorithms are used for rational, hypergeometric,
 -rational, and other types of indefinite, finite, and infinite sums including Adamchik techniques for returning answers in terms of generalized hypergeometric functions.
-rational, and other types of indefinite, finite, and infinite sums including Adamchik techniques for returning answers in terms of generalized hypergeometric functions.
- The algorithms in the Wolfram Language cover at least 90% of the sums in standard reference books such as Gradshteyn–Ryzhik.
- Products are done using special algorithms for polynomial, rational,
 -rational, hypergeometric, periodic, and other classes as well as by using pattern matching.
-rational, hypergeometric, periodic, and other classes as well as by using pattern matching.
Series and Limits
- Series works by recursively composing series expansions of functions with series expansions of their arguments.
- Assumptions in limits and series are processed using a general-purpose evaluate-with-assumptions mechanism built into Refine and Simplify.
Recurrence Equations
- RSolve solves systems of linear equations with constant coefficients using matrix powers.
- Linear equations with polynomial coefficients whose solutions can be given as hypergeometric terms are solved using van Hoeij algorithms.
- Systems of linear equations with rational function coefficients whose solutions can be given as rational functions are solved using Abramov–Bronstein elimination algorithms.
- Nonlinear equations are solved by transformation of variables, Göktaş symmetry reduction methods or Germundsson trigonometric power methods.
- The algorithms in the Wolfram Language cover most of the ordinary,
 -, and functional difference equations ever discussed in the mathematical literature.
-, and functional difference equations ever discussed in the mathematical literature.
- For difference-algebraic equations, a method based on isolating singular parts by core nilpotent decomposition is used.
Graphics
- The 3D renderer uses two different methods of sorting polygons. For graphics scenes that include no transparency, a hardware-accelerated depth buffer is used. Otherwise, the renderer uses a binary space partition tree to split and sort polygons from any viewpoint. The BSP tree is slower to create and is not hardware accelerated, but it provides the most general ability to support polygons.
- Graphics in notebooks are the result of typesetting rules in MakeBoxes that have been applied to kernel graphics primitives. MakeBoxes typically preserves the structure of kernel graphics.
- Graphics may be evaluated in the Wolfram Language. By default, they will often evaluate to their kernel representation, although additional evaluation rules may be applied by overloading MakeExpression.
- Notebooks use a custom platform-independent bitmap image format. This format is used for bitmap cells and for caching the appearance of graphics output.
- On systems where antialiasing of graphics is supported, the front end selectively uses antialiasing to ensure the best possible rendering of 2D graphics. 3D graphics are uniformly antialiased depending upon the setting in the Preferences dialog.
Visualization
- In Version 6, warning messages involving functions returning non-numeric values are Off by default. These messages include Plot::plnr, ParametricPlot::pptr, and ParametricPlot3D::pp3tr.
- The visualization functions return in most cases a GraphicsComplex object.
- As GraphicsComplex is a vertex-based construct, functions such as ListDensityPlot will behave completely differently than in Version 5. Functions such as ArrayPlot and ReliefPlot can be used to get results similar to ListDensityPlot in Version 5.
- Plotting functions include several state-of-the-art geometric algorithms, with special emphasis on visual quality.
- Special code that attempts to speed up the plotting process at the cost of quality is used by default in Manipulate constructions. Options such as PerformanceGoal, PlotPoints, and MaxRecursion allow full control over the optimization process.
- Exclusions make use of highly sophisticated symbolic processing. The first time a plotting function with the Exclusions option is used, the system needs to load the Exclusions Package, which causes a slight delay.
- The exclusions functionality handles jumps and singularities by using numerical offsetting around points and curves. In some cases undesired gaps may appear. Use Exclusions->None to avoid such artifacts.
- When ColorFunction is used for curves (such as in Plot and ParametricPlot), very large expressions can be created because an individual color directive for each segment is generated.
- Adaptive refinement is based purely on geometric properties. For curves with a ColorFunction, it may be necessary to increase the number of PlotPoints to get smooth color transitions.
- MeshFunctions uses a numerical method to determine the cutting values by checking the sign, so functions like Abs and Boole cannot be used to drive the construction of the mesh.
- Mesh lines and contour lines are an integral part of the geometry, not overlays. As a consequence, large numbers of mesh lines or contours will generate a large number of polygons in the corresponding GraphicsComplex.
- In function visualization using functions such as Plot, ParametricPlot, Plot3D, and ParametricPlot3D, a Table of functions is interpreted as vectors. Therefore the style will be the same for all the curves or surfaces. Use Evaluate to explicitly expand the table as individual functions.
- In ContourPlot, the value of MaxRecursion is applied first to determine the main features, and then a second recursion stage is used to smooth out the contour curves. Note that a value of MaxRecursion->n can possibly generate up to
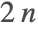 levels of recursion.
levels of recursion.
- ContourPlot3D can identify algebraic functions and perform a symbolic analysis to determine all the singularities. In some cases, the default value of MaxRecursion may not be enough to resolve all the detail along singularities. In such cases, increase MaxRecursion.
- ContourLabels are placed in such a way as to maximize the minimum distance between the labels. The text style and text size are not considered in determining the optimal locations.
- For irregular data, ListPlot3D constructs a Delaunay triangulation. For large coordinate values, some points might be dropped. Rescaling the data will improve the result.
- ListSurfacePlot3D is a reconstruction function that tries to find a surface as close as possible to the data. Regions with a low number of sampled values will introduce holes on the surface.
- Data points in ListSurfacePlot3D are used to construct a distance function that is used to find the zero-level surface. The original points are not part of the final result.
Front End
- The front end uses WSTP both for communication with the kernel, and for communication between its different internal components.
- All menu items and other functions in the front end are specified using Wolfram Language expressions.
- Documentation is authored in Wolfram System notebooks. It is then processed by special Wolfram Language programs to create the final documentation notebooks and the online documentation website as well as other Wolfram Language content, such as the database of syntax coloring information and the usage messages.
- The front end maintains syntax coloring information about user variables by querying the kernel after evaluations are finished. When several evaluations are queued, the query may not happen after every single evaluation. The query always happens after the last evaluation in the queue.
Notebooks
- Notebook files contain additional cached outline information in the form of Wolfram Language comments. This information makes possible efficient random access.
- Incremental saving of notebooks is done so as to minimize rewriting of data, moving data already written out whenever possible.
- Platform-independent double-buffering is used by default to minimize flicker when window contents are updated.
- All characters are represented internally and in files using Unicode values. Mapping tables for many encodings are included to support communication with system interfaces and third-party software that use other encodings.
- When copying text to the clipboard, many technical characters and all private-space characters are encoded using their verbose long names instead of their Unicode values to improve readability by software that may not be able to properly render those characters. All alphabetical characters are encoded in Unicode regardless of the system's localized language.
- Spell checking is done using algorithms and a 100,000-word English dictionary that includes standard English, technical terms, and words used by the Wolfram Language. Spelling correction is done using textual, phonetic, and keyboard distance metrics.
- Hyphenation is done using the Liang hyphenation algorithm and the standard TeX patterns for English hyphenation.
Dynamic Evaluation
- The front end establishes three unique links to each kernel it communicates with. One link is used for regular evaluations initiated by the user, while the other two links are used for updating the values of Dynamic objects.
- When the front end formats a Dynamic object, it sends the evaluation to the kernel. The kernel registers all variables used in the Dynamic evaluation in a dependency table.
- When a variable in the kernel changes, the kernel sends a message to the front end to invalidate any Dynamic object depending on that variable, then removes the dependency information from its dependency table.
- The front end has a dependency table for tracking Dynamic objects that depend upon values that can only be determined by the front end. This includes Dynamic objects that depend upon MousePosition, ControllerState or any CurrentValue expression that probes a front end object.
- The front end only sends invalidated Dynamic objects to the kernel when it needs to do so in order to update a notebook window. For example, Dynamic objects that have been scrolled offscreen or have been hidden by other windows are not refreshed.
- Not all Dynamic evaluations require the front end to send an evaluation to the kernel. The front end automatically determines if the evaluation is trivial enough to be computed by a mini-evaluator inside the front end.
- If a Dynamic evaluation occurs during a regular evaluation, the kernel pauses the regular evaluation in order to process the Dynamic evaluation. The mechanism for pausing the kernel evaluation is the same mechanism used for interrupting the kernel and for evaluating in subsessions.
- The front end wraps dynamic evaluations sent to the kernel in TimeConstrained, with the timeout set to the value of the DynamicEvaluationTimeout option. The front end also wraps dynamic evaluations in constructs to resolve DynamicModule variables if necessary.
WSTP
- The Wolfram Symbolic Transfer Protocol (WSTP) is a presentation-level protocol that can be layered on top of any transport medium, both message-based and stream-based.
- WSTP encodes data in a compressed format when it determines that both ends of a link are on compatible computer systems.
Expression Formatting
- The front end uses a directed acyclic graph to represent the box structure of formatted expressions.
- Graphics and typesetting are implemented in the same formatting language, which allows them to work together seamlessly.
- Line breaking is globally optimized throughout expressions, based on a method similar to the one used for text layout in TeX.
- During input, line breaking is set up so that small changes to expressions rarely cause large-scale reformatting; if the input needs to jump, an elliptical cursor tracker momentarily appears to guide the eye.