is the exponential constant ![]() (base of natural logarithms), with numerical value
(base of natural logarithms), with numerical value ![]() .
.


E 
is the exponential constant ![]() (base of natural logarithms), with numerical value
(base of natural logarithms), with numerical value ![]() .
.
Details
- Mathematical constant treated as numeric by NumericQ and as a constant by D.
- E can be evaluated to any numerical precision using N.
- E can be entered in StandardForm and InputForm as ,
 ee
ee or \[ExponentialE].
or \[ExponentialE]. - In StandardForm and TraditionalForm, E is printed as .
Background & Context
- E is the symbol representing the base of the natural logarithm Log. It is also known as Euler's number and can be input as \[ExponentialE]. E has a number of equivalent definitions in mathematics, including as the infinite sum of reciprocal factorials over non-negative integers
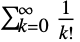 and as the limiting value
and as the limiting value 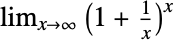 . It has a numerical value
. It has a numerical value 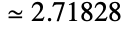 . With the possible exception of Pi, E is the most important constant in mathematics. It appears in many sums, products, integrals, in equations involving the compounding of interest, in growth laws involving exponential growth or decay, and in formulas from a wide range of other mathematical and scientific fields.
. With the possible exception of Pi, E is the most important constant in mathematics. It appears in many sums, products, integrals, in equations involving the compounding of interest, in growth laws involving exponential growth or decay, and in formulas from a wide range of other mathematical and scientific fields. - The exponential function Exp[x] is converted to E^x. When E is used as a symbol, it is propagated as an exact quantity. Expansion and simplification of complicated expressions involving E may require use of functions such as FunctionExpand and FullSimplify.
- Euler proved that E is irrational (meaning it cannot be expressed as a ratio of any two integers) and Hermite subsequently established that it is transcendental (meaning it is not the root of any integer polynomial). However, E is the "least" transcendental number possible since it has irrationality measure of 2. lt is not known if E is normal (meaning the digits in its base-b expansion are equally distributed) to any base. Despite its extensive appearance in various closed-form sums and integrals, E is conjectured to not be a Kontsevich–Zagier period (meaning it is not the value of an absolutely convergent integral of any univariate or multivariate rational function with rational coefficients over algebraically-specified domains in
 ).
). - E can be evaluated to arbitrary numerical precision using N. In fact, calculating the first million decimal digits of E takes only a fraction of a second on a modern desktop computer. RealDigits can be used to return a list of digits of E and ContinuedFraction to obtain terms of its continued fraction expansion.
Related Guides
Related Links
History
Introduced in 1988 (1.0) | Updated in 1996 (3.0) ▪ 1999 (4.0) ▪ 2000 (4.1) ▪ 2002 (4.2)
Text
Wolfram Research (1988), E, Wolfram Language function, https://reference.wolfram.com/language/ref/E.html (updated 2002).
CMS
Wolfram Language. 1988. "E." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2002. https://reference.wolfram.com/language/ref/E.html.
APA
Wolfram Language. (1988). E. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/E.html
BibTeX
@misc{reference.wolfram_2025_e, author="Wolfram Research", title="{E}", year="2002", howpublished="\url{https://reference.wolfram.com/language/ref/E.html}", note=[Accessed: 14-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_e, organization={Wolfram Research}, title={E}, year={2002}, url={https://reference.wolfram.com/language/ref/E.html}, note=[Accessed: 14-January-2026]}