ListConvolve

ListConvolve[ker,list]

forms the convolution of the kernel ker with list.

ListConvolve[ker,list,k]

forms the cyclic convolution in which the k^(th) element of ker is aligned with each element in list.

ListConvolve[ker,list,{kL,kR}]

forms the cyclic convolution whose first element contains list[[1]]ker[[kL]] and whose last element contains list[[-1]]ker[[kR]].

ListConvolve[ker,list,klist,p]

forms the convolution in which list is padded at each end with repetitions of the element p.

ListConvolve[ker,list,klist,{p1,p2,…}]

forms the convolution in which list is padded at each end with cyclic repetitions of the pi.

ListConvolve[ker,list,klist,padding,g,h]

forms a generalized convolution in which g is used in place of Times and h in place of Plus.

ListConvolve[ker,list,klist,padding,g,h,lev]

forms a convolution using elements at level lev in ker and list.

Details

  • With kernel Kr and list as, ListConvolve[ker,list] computes 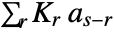, where the limits of the sum are such that the kernel never overhangs either end of the list.
  • ListConvolve[ker,list] gives a result of length Length[list]-Length[ker]+1.
  • ListConvolve[ker,list] allows no overhangs and is equivalent to ListConvolve[ker,list,{-1,1}].
  • ListConvolve[ker,list,k] is equivalent to ListConvolve[ker,list,{k,k}].
  • The values of kL and kR in ListConvolve[ker,list,{kL,kR}] determine the amount of overhang to allow at each end of list.
  • Common settings for {kL,kR} are:
  • {-1,1}no overhangs (default)
    {-1,-1}maximal overhang at the right‐hand end
    {1,1}maximal overhang at the left‐hand end
    {1,-1}maximal overhangs at both beginning and end
  • With maximal overhang at one end only, the result from ListConvolve is the same length as list.
  • ListConvolve[ker,list,{kL,kR},padlist] effectively lays down repeated copies of padlist, then superimposes one copy of list on them and forms a convolution of the result.
  • Common settings for padlist are:
  • ppad with repetitions of a single element
    {p1,p2,…}pad with cyclic repetitions of a sequence of elements
    listpad by treating list as cyclic (default)
    {}do no padding
  • ListConvolve works with multidimensional kernels and lists of data.
  • ListConvolve[ker,list,{{kL 1,kL 2,…},{kR 1,kR 2,…}}] forms the cyclic convolution whose {1,1,…} element contains ker[[kL 1,kL 2,…]]list[[1,1,…]], and whose {-1,-1,…} element contains ker[[kR 1,kR 2,…]]list[[-1,-1,…]].
  • {kL,kR} is taken to be equivalent to {{kL,kL,…},{kR,kR,…}}.
  • When a function h is specified to use in place of Plus, explicit nested h expressions are generated with a depth equal to the depth of ker.
  • ListConvolve works with exact numbers and symbolic data as well as approximate numbers.

Examples

open allclose all

Basic Examples  (4)

Convolve a kernel {x,y} with a list of data:

Make a cyclic convolution the same length as the original data:

Align element 2 in the kernel with successive elements in the data:

Pad with zzz instead of using the data cyclically:

Two-dimensional convolution:

Scope  (9)

Overhangs and Alignments  (4)

"Slide" the kernel along the data, allowing no overhangs:

Maximal overhang at the beginning; none at the end:

Maximal overhang at the end; none at the beginning:

Maximal overhangs at both beginning and end:

Align element 1 of the kernel with the first element of the data:

Align element 2 of the kernel with the first element of the data:

Align element 3 of the kernel with the first element of the data:

Align the last element of the kernel with the first element of the data:

Align the first element of the kernel with both the first and last elements of the data:

Align element 2 of the kernel with the first element of the data:

Align element 2 of the kernel with the last element of the data:

Data Padding  (2)

Use padding aa:

Cyclically use a list of padding elements:

Higher Dimensions  (3)

Allow no overhangs:

Align with the {1,1} elements of the kernel and data:

The result has the same dimensions as the input data:

Give a different overhang in each dimension:

Generalizations & Extensions  (4)

ListConvolve works with sparse arrays:

Use f in place of Times:

Use g in place of Plus:

Use f and g in place of Times and Plus, with empty data padding:

ListConvolve works with TimeSeries:

Applications  (9)

Find a moving average:

Or use the MovingAverage function:

Smooth noisy data:

Find the autocorrelation of a list:

Apply a simple image processing filter:

Multiply polynomials by convolving coefficient lists:

Multiply numbers by convolving digit lists:

Pascal's triangle:

Additive cellular automaton in base 5:

Fast multiplication of high‐degree polynomials:

Use ListConvolve with maximal overhangs and zero padding:

Properties & Relations  (8)

Generate two random vectors:

A function for constructing a circulant matrix from a vector:

Cyclic convolution is equivalent to multiplication with a circulant matrix:

Cyclic convolution is also equivalent to multiplication in the discrete Fourier transform domain:

Generate two random vectors:

A function for constructing a lower triangular Toeplitz matrix from a vector:

Cyclic convolution with zero-padding is equivalent to multiplication with a lower triangular Toeplitz matrix:

Convolve with a single element:

A kernel of the same length as the data, with no overhangs, is like a reversed dot product:

Successive differences:

Align with successive elements:

Varying alignments:

Varying alignments, with padding:

Possible Issues  (1)

By default, the output is not the same length as the input:

Use overhangs to make the output the same length as the input:

Use overhangs to do the same in 2D:

Wolfram Research (1999), ListConvolve, Wolfram Language function, https://reference.wolfram.com/language/ref/ListConvolve.html.

Text

Wolfram Research (1999), ListConvolve, Wolfram Language function, https://reference.wolfram.com/language/ref/ListConvolve.html.

CMS

Wolfram Language. 1999. "ListConvolve." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ListConvolve.html.

APA

Wolfram Language. (1999). ListConvolve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ListConvolve.html

BibTeX

@misc{reference.wolfram_2024_listconvolve, author="Wolfram Research", title="{ListConvolve}", year="1999", howpublished="\url{https://reference.wolfram.com/language/ref/ListConvolve.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_listconvolve, organization={Wolfram Research}, title={ListConvolve}, year={1999}, url={https://reference.wolfram.com/language/ref/ListConvolve.html}, note=[Accessed: 17-November-2024 ]}