GradientFilter

GradientFilter[data,r]

gives the magnitude of the gradient of data, computed using discrete derivatives of a Gaussian of sample radius r.

GradientFilter[data,{r,σ}]

uses a Gaussian with standard deviation σ.

GradientFilter[data,{{r1,r2,…},…}]

uses a Gaussian with radius ri at level i in data.

Details and Options

  • GradientFilter is commonly used to detect regions of rapid change in signals and images.
  • For a single-channel image and for data, the gradient magnitude is the Euclidean norm of the gradient 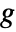at a pixel position, approximated using discrete derivatives of Gaussians in each dimension.
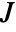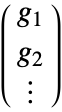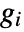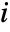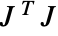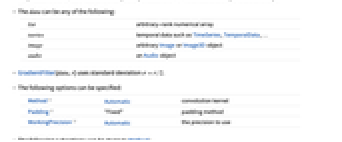
  • For multichannel images, the Jacobian matrix is , where is the gradient for channel . Gradient magnitude is the square root of the largest eigenvalue of , returned as a single-channel image.
  • The data can be any of the following:
  • listarbitrary-rank numerical array
    tseriestemporal data such as TimeSeries, TemporalData, …
    imagearbitrary Image or Image3D object
    audioan Audio object
  • GradientFilter[data,r] uses standard deviation .
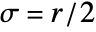  • The following options can be specified:
  • Method Automaticconvolution kernel
    Padding "Fixed"padding method
    WorkingPrecision Automaticthe precision to use
  • The following suboptions can be given to Method:
  • "DerivativeKernel""Bessel"convolution kernel
    "NonMaxSuppression"Falsewhether to use non-maximum suppression
  • Possible settings for "DerivativeKernel" include:
  • "Bessel"standardized Bessel derivative kernel, used for Canny edge detection
    "Gaussian"standardized Gaussian derivative kernel, used for Canny edge detection
    "ShenCastan"first-order derivatives of exponentials
    "Sobel"binomial generalizations of the Sobel edge-detection kernels
    {kernel1,kernel2,…}explicit kernels specified for each dimension
  • GradientFilter[data,…] by default gives an array, audio object or image of the same dimensions as data.
  • With setting Padding->None, GradientFilter[data,…] normally gives an array, audio object or image smaller than data.
  • GradientFilter[image,…] returns an image of a real type.

Examples

open allclose all

Basic Examples  (3)

Gradient filter of a grayscale image:

Gradient filtering of a 3D image:

Apply gradient filtering to a vector of numbers:

Scope  (10)

Data  (6)

Gradient filter of a numeric vector:

Gradient filter of a numeric matrix:

Filter a TimeSeries:

Filter an Audio signal:

Filter a color image:

Filter a 3D image:

Parameters  (4)

Gradient filtering using increasing radii:

Use different vertical and horizontal radii:

Gradient derivative of a 3D image in the vertical direction only:

Filtering of the horizontal planes only:

The default standard deviation is :

Specify a different :

Options  (9)

Method  (3)

Compute the gradient magnitude using the default Bessel method:

Use the Shen–Castan method:

Compute the gradient magnitude using Prewitt kernels:

Typically, corners are rounded during gradient filtering:

The Shen–Castan method gives a better corner localization at large scales:

By default, non-max suppression is not applied:

Non-max suppression gives only the ridges of gradient lines:

Use Shen-Castan method with no-max suppression:

Padding  (2)

GradientFilter using different padding methods:

Padding->None normally returns an image smaller than the input image:

WorkingPrecision  (4)

MachinePrecision is by default used with integer arrays:

Perform an exact computation instead:

With real arrays, by default the precision of the input is used:

Specify the precision to use:

With symbolic arrays, exact computation is used:

WorkingPrecision is ignored when filtering images:

An image of a real type is always returned:

Applications  (4)

Use gradient filtering to find edges:

Compute an unsharp mask:

Add the unsharp mask to the original image:

Use gradient filtering as a preprocessing step for watershed segmentation:

Get borders from a colored map:

Properties & Relations  (4)

GradientFilter of a vector is the absolute value of the Gaussian first derivative of the vector:

GradientFilter of a grayscale image is the square root of the sum of squares of Gaussian first derivatives in each dimension of an image:

Impulse responses of gradient filter for selected radii:

Gradient filter impulse responses in 2D:

Impulse responses of gradient filter using different "DerivativeKernel" settings:

Gradient filtering of a binary image gives a grayscale image of a real type:

Possible Issues  (1)

Gradient filtering usually results in a dark image with small pixel values:

Adjusting for brightness creates a more visible image gradient:

Neat Examples  (2)

Compute and visualize multiscale gradient filtering:

An artistic effect based on image gradients:

Wolfram Research (2008), GradientFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/GradientFilter.html (updated 2016).

Text

Wolfram Research (2008), GradientFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/GradientFilter.html (updated 2016).

CMS

Wolfram Language. 2008. "GradientFilter." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/GradientFilter.html.

APA

Wolfram Language. (2008). GradientFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GradientFilter.html

BibTeX

@misc{reference.wolfram_2024_gradientfilter, author="Wolfram Research", title="{GradientFilter}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/GradientFilter.html}", note=[Accessed: 12-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_gradientfilter, organization={Wolfram Research}, title={GradientFilter}, year={2016}, url={https://reference.wolfram.com/language/ref/GradientFilter.html}, note=[Accessed: 12-November-2024 ]}