GradientFilter
GradientFilter[data,r]
gives the magnitude of the gradient of data, computed using discrete derivatives of a Gaussian of sample radius r.
GradientFilter[data,{r,σ}]
uses a Gaussian with standard deviation σ.
GradientFilter[data,{{r1,r2,…},…}]
uses a Gaussian with radius ri at level i in data.
Details and Options


- GradientFilter is commonly used to detect regions of rapid change in signals and images.
- For a single-channel image and for data, the gradient magnitude is the Euclidean norm of the gradient
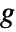 at a pixel position, approximated using discrete derivatives of Gaussians in each dimension.
at a pixel position, approximated using discrete derivatives of Gaussians in each dimension. - For multichannel images, the Jacobian matrix
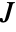 is
is 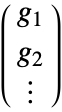 , where
, where 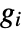 is the gradient for channel
is the gradient for channel 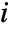 . Gradient magnitude is the square root of the largest eigenvalue of
. Gradient magnitude is the square root of the largest eigenvalue of 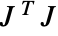 , returned as a single-channel image.
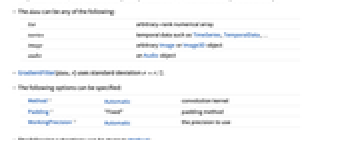
, returned as a single-channel image. - The data can be any of the following:
-
list arbitrary-rank numerical array tseries temporal data such as TimeSeries, TemporalData, … image arbitrary Image or Image3D object audio an Audio object - GradientFilter[data,r] uses standard deviation
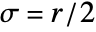 .
. - The following options can be specified:
-
Method Automatic convolution kernel Padding "Fixed" padding method WorkingPrecision Automatic the precision to use - The following suboptions can be given to Method:
-
"DerivativeKernel" "Bessel" convolution kernel "NonMaxSuppression" False whether to use non-maximum suppression - Possible settings for "DerivativeKernel" include:
-
"Bessel" standardized Bessel derivative kernel, used for Canny edge detection "Gaussian" standardized Gaussian derivative kernel, used for Canny edge detection "ShenCastan" first-order derivatives of exponentials "Sobel" binomial generalizations of the Sobel edge-detection kernels {kernel1,kernel2,…} explicit kernels specified for each dimension - GradientFilter[data,…] by default gives an array, audio object or image of the same dimensions as data.
- With setting Padding->None, GradientFilter[data,…] normally gives an array, audio object or image smaller than data.
- GradientFilter[image,…] returns an image of a real type.

Examples
open allclose allBasic Examples (3)
Scope (10)
Data (6)
Gradient filter of a numeric vector:
Gradient filter of a numeric matrix:
Filter a TimeSeries:
Filter an Audio signal:
Options (9)
Method (3)
Compute the gradient magnitude using the default Bessel method:
Compute the gradient magnitude using Prewitt kernels:
Typically, corners are rounded during gradient filtering:
The Shen–Castan method gives a better corner localization at large scales:
By default, non-max suppression is not applied:
Non-max suppression gives only the ridges of gradient lines:
Padding (2)
GradientFilter using different padding methods:
Padding->None normally returns an image smaller than the input image:
WorkingPrecision (4)
MachinePrecision is by default used with integer arrays:
Perform an exact computation instead:
With real arrays, by default the precision of the input is used:
With symbolic arrays, exact computation is used:
WorkingPrecision is ignored when filtering images:
Applications (4)
Properties & Relations (4)
GradientFilter of a vector is the absolute value of the Gaussian first derivative of the vector:
GradientFilter of a grayscale image is the square root of the sum of squares of Gaussian first derivatives in each dimension of an image:
Impulse responses of gradient filter for selected radii:
Gradient filter impulse responses in 2D:
Impulse responses of gradient filter using different "DerivativeKernel" settings:
Gradient filtering of a binary image gives a grayscale image of a real type:
Possible Issues (1)
Text
Wolfram Research (2008), GradientFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/GradientFilter.html (updated 2016).
CMS
Wolfram Language. 2008. "GradientFilter." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/GradientFilter.html.
APA
Wolfram Language. (2008). GradientFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GradientFilter.html