GraphDifference

GraphDifference[g1,g2]

gives the graph difference of the graphs g1 and g2.

GraphDifference[{vw,…},…]

uses rules vw to specify the graph g.

Details and Options

  • The graph difference Graph[v1,e1]∖Graph[v2,e2] is given by Graph[v1⋃v2,e1∖ e2].
  • GraphDifference works with undirected graphs, directed graphs, multigraphs, and mixed graphs.

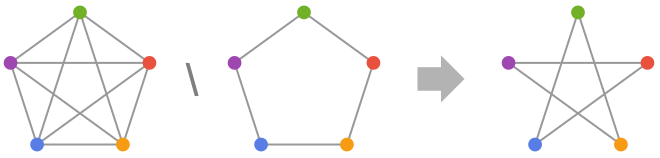
Examples

open allclose all

Basic Examples  (1)

Obtain the graph difference of two graphs:

Highlight the graph difference:

Scope  (5)

GraphDifference works with undirected graphs:

Directed graphs:

Multigraphs:

Mixed graphs:

Use rules to specify the graph:

Properties & Relations  (6)

The vertices of the graph difference are the union of the vertices of the graphs:

The edges of the graph difference are the complement of the edges of the graphs:

The graph difference of any graph and itself is an empty graph:

The graph difference of any graph and its CompleteGraph is isomorphic to the complement of the graph:

The GraphDifference of two graphs has the same vertices as GraphUnion:

The GraphDifference of two graphs has the same vertices as GraphIntersection:

Wolfram Research (2010), GraphDifference, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphDifference.html (updated 2015).

Text

Wolfram Research (2010), GraphDifference, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphDifference.html (updated 2015).

CMS

Wolfram Language. 2010. "GraphDifference." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GraphDifference.html.

APA

Wolfram Language. (2010). GraphDifference. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphDifference.html

BibTeX

@misc{reference.wolfram_2024_graphdifference, author="Wolfram Research", title="{GraphDifference}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GraphDifference.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_graphdifference, organization={Wolfram Research}, title={GraphDifference}, year={2015}, url={https://reference.wolfram.com/language/ref/GraphDifference.html}, note=[Accessed: 21-November-2024 ]}