WOLFRAM

Wolfram Language & System Documentation Center

IndependentVertexSetQ[g,vlist]

yields True if the vertex list vlist is an independent vertex set in the graph g, and False otherwise.

Details
Details and Options Details and Options
Examples  
Basic Examples  
Scope  
Applications  
Properties & Relations  
See Also
Related Guides
History
Cite this Page

IndependentVertexSetQ

IndependentVertexSetQ[g,vlist]

yields True if the vertex list vlist is an independent vertex set in the graph g, and False otherwise.

Details

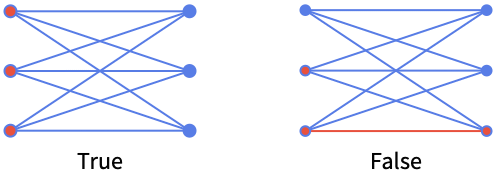
  • An independent vertex set is a set of vertices that are never incident to the same edge.
  • IndependentVertexSetQ works with undirected graphs, directed graphs, multigraphs, and mixed graphs.

Examples

open all close all

Basic Examples  (2)

Test whether a set of vertices is an independent vertex set:

Not all sets of vertices are independent vertex sets in a graph:

Scope  (5)

Test undirected graphs:

Directed graphs:

Multigraphs:

Mixed graphs:

IndependentVertexSetQ works with large graphs:

Applications  (2)

Enumerate all independent vertex sets for a cycle graph:

Enumerate all subsets of vertices and select the ones that are independent vertex sets:

Highlight independent vertex sets:

Enumerate all maximum independent vertex sets for a Petersen graph:

Find the size of a maximum independent vertex set:

Enumerate all maximum independent vertex sets:

Highlight maximum independent sets:

Properties & Relations  (4)

A largest independent vertex set can be found using FindIndependentVertexSet:

The complement of an independent vertex set is a vertex cover:

The complement subgraph given by an independent vertex set is complete:

Bipartite graphs have equal-length edge covers and independent vertex sets:

Wolfram Research (2010), IndependentVertexSetQ, Wolfram Language function, https://reference.wolfram.com/language/ref/IndependentVertexSetQ.html (updated 2014).

Text

Wolfram Research (2010), IndependentVertexSetQ, Wolfram Language function, https://reference.wolfram.com/language/ref/IndependentVertexSetQ.html (updated 2014).

CMS

Wolfram Language. 2010. "IndependentVertexSetQ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/IndependentVertexSetQ.html.

APA

Wolfram Language. (2010). IndependentVertexSetQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/IndependentVertexSetQ.html

BibTeX

@misc{reference.wolfram_2025_independentvertexsetq, author="Wolfram Research", title="{IndependentVertexSetQ}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/IndependentVertexSetQ.html}", note=[Accessed: 13-August-2025]}

BibLaTeX

@online{reference.wolfram_2025_independentvertexsetq, organization={Wolfram Research}, title={IndependentVertexSetQ}, year={2014}, url={https://reference.wolfram.com/language/ref/IndependentVertexSetQ.html}, note=[Accessed: 13-August-2025]}