LocationTest[data]
tests whether the mean or median of the data is zero.
LocationTest[{data1,data2}]
tests whether the means or medians of data1 and data2 are equal.
LocationTest[dspec,μ0]
tests a location measure against μ0.
LocationTest[dspec,μ0,"property"]
returns the value of "property".


LocationTest
LocationTest[data]
tests whether the mean or median of the data is zero.
LocationTest[{data1,data2}]
tests whether the means or medians of data1 and data2 are equal.
LocationTest[dspec,μ0]
tests a location measure against μ0.
LocationTest[dspec,μ0,"property"]
returns the value of "property".
Details and Options




- LocationTest performs a hypothesis test on data with null hypothesis
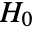 that the true population location parameter is some value
that the true population location parameter is some value 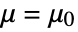 , and alternative hypothesis
, and alternative hypothesis 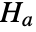 that
that 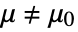 .
. - Given data1 and data2, LocationTest tests null hypothesis
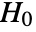 against alternative hypothesis
against alternative hypothesis 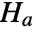 , where
, where 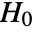 and
and 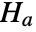 are defined for each test accordingly.
are defined for each test accordingly. - By default, a probability value or
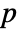 -value is returned.
-value is returned. - A small
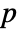 -value suggests that it is unlikely that
-value suggests that it is unlikely that 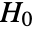 is true.
is true. - The data in dspec can be univariate {x1,x2,…} or multivariate {{x1,y1,…},{x2,y2,…},…}.
- The argument μ0 can be a real number or a real vector with length equal to the dimension of the data.
- LocationTest[dspec] will choose the most powerful test that applies to dspec.
- LocationTest[dspec,Automatic] is equivalent to
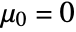 .
. - LocationTest[dspec,μ0,All] will choose all tests that apply to dspec.
- LocationTest[dspec,μ0,"test"] reports the
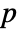 -value according to "test".
-value according to "test". - Tests based on means assume the data in dspec is normally distributed. Some tests assume the data is symmetric about a common median. Tests that do not assume symmetry or normality are classified as robust.
- A paired sample test assumes equal-length dependent data.
- The following tests can be used:
-
"PairedT" normality paired sample test with unknown variance "PairedZ" normality paired sample test with known variance "Sign" robust median test for one sample or matched pairs "SignedRank" symmetry median test for one sample or matched pairs "T" normality mean test for one or two samples "MannWhitney" symmetry median test for two independent samples "Z" normality mean test with known variance - The "T" test performs Student
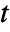 -test for univariate data and Hotelling's
-test for univariate data and Hotelling's 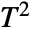 test for multivariate data.
test for multivariate data. - The "Z" test performs a
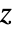 -test assuming the sample variance is the known variance for univariate data and Hotelling's
-test assuming the sample variance is the known variance for univariate data and Hotelling's 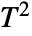 test assuming the sample covariance is the known covariance for multivariate data.
test assuming the sample covariance is the known covariance for multivariate data. - The "PairedT" and "PairedZ" tests perform "T" and "Z" tests on the paired differences of two datasets. A single dataset is treated as a list of differences.
- LocationTest[dspec,μ0,"HypothesisTestData"] returns a HypothesisTestData object htd that can be used to extract additional test results and properties using the form htd["property"].
- LocationTest[dspec,μ0,"property"] can be used to directly give the value of "property".
- Properties related to the reporting of test results include:
-
"AllTests" list of all applicable tests "AutomaticTest" test chosen if Automatic is used "DegreesOfFreedom" the degrees of freedom used in a test "PValue" list of 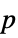 -values
-values"PValueTable" formatted table of 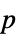 -values
-values"ShortTestConclusion" a short description of the conclusion of a test "TestConclusion" a description of the conclusion of a test "TestData" list of pairs of test statistics and 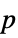 -values
-values"TestDataTable" formatted table of 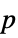 -values and test statistics
-values and test statistics"TestStatistic" list of test statistics "TestStatisticTable" formatted table of test statistics - The following options can be used:
-
AlternativeHypothesis "Unequal" the inequality for the alternative hypothesis MaxIterations Automatic max iterations for multivariate median tests Method Automatic the method to use for computing 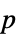 -values
-valuesSignificanceLevel 0.05 cutoff for diagnostics and reporting VerifyTestAssumptions Automatic what assumptions to verify - For tests of location, a cutoff
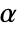 is chosen such that
is chosen such that 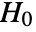 is rejected only if
is rejected only if 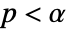 . The value of
. The value of 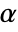 used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. This value
used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. This value 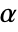 is also used in diagnostic tests of assumptions including tests for normality, equal variance, and symmetry. By default,
is also used in diagnostic tests of assumptions including tests for normality, equal variance, and symmetry. By default, 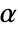 is set to 0.05.
is set to 0.05. - Named settings for VerifyTestAssumptions in LocationTest include:
-
"EqualVariance" verify that data1 and data2 have equal variance "Normality" verify that all data is normally distributed "Symmetry" verify symmetry about a common median
Examples
open all close allBasic Examples (3)
Test whether the mean or median of a population is zero using a collection of tests:
Test whether the means of two populations differ by 2:
At the 0.05 level, ![]() is significantly different from 2:
is significantly different from 2:
Compare the locations of multivariate populations:
At the 0.05 level, ![]() is not significantly different from {1,2}:
is not significantly different from {1,2}:
Scope (17)
Testing (13)
The ![]() -values are typically large when the mean is close to 0:
-values are typically large when the mean is close to 0:
The ![]() -values are typically small when the mean is far from 0:
-values are typically small when the mean is far from 0:
Using Automatic is equivalent to testing for a mean of zero:
The ![]() -values are typically large when the mean is close to μ0:
-values are typically large when the mean is close to μ0:
The ![]() -values are typically small when the mean is far from μ0:
-values are typically small when the mean is far from μ0:
Test whether the mean vector of a multivariate population is the zero vector:
Alternatively, test against {0.1,0,-0.05,0}:
Using Automatic applies the generally most powerful appropriate test:
The property "AutomaticTest" can be used to determine which test was chosen:
The ![]() -values are generally small when the locations are not equal:
-values are generally small when the locations are not equal:
The ![]() -values are generally large when the locations are equal:
-values are generally large when the locations are equal:
The order of the datasets affects the test results:
Test whether the mean difference vector of two multivariate populations is the zero vector:
Alternatively, test against {1,0,-1,0}:
Perform a particular test for equal locations:
Any number of tests can be performed simultaneously:
Perform all tests appropriate to the data simultaneously:
Use the property "AllTests" to identify which tests were used:
Create a HypothesisTestData object for repeated property extraction:
The properties available for extraction:
Extract some properties from a HypothesisTestData:
The ![]() -value and test statistic from a
-value and test statistic from a ![]() -type test:
-type test:
Reporting (4)
Tabulate the results from a selection of tests:
A full table of all appropriate test results:
A table of selected test results:
Retrieve the entries from a test table for customized reporting:
The ![]() -values are above 0.05, so there is not enough evidence to reject
-values are above 0.05, so there is not enough evidence to reject ![]() at that level:
at that level:
Tabulate ![]() -values for a test or group of tests:
-values for a test or group of tests:
A table of ![]() -values from all appropriate tests:
-values from all appropriate tests:
A table of ![]() -values from a subset of tests:
-values from a subset of tests:
Report the test statistic from a test or group of tests:
Options (20)
AlternativeHypothesis (3)
Method (6)
By default, ![]() -values are computed using asymptotic test statistic distributions:
-values are computed using asymptotic test statistic distributions:
For univariate median-based tests, ![]() -values can be obtained using permutation methods:
-values can be obtained using permutation methods:
Set the number of permutations to use:
By default, ![]() random permutations are used:
random permutations are used:
For some tests, the permutation result is exact:
The result is not affected by the number of permutations when exact tests are used:
For mean-based tests, the ![]() -value is exact under the assumptions of the test:
-value is exact under the assumptions of the test:
SignificanceLevel (3)
VerifyTestAssumptions (7)
By default, normality and equal variance are tested when appropriate:
If assumptions are not checked, some test results may differ:
Diagnostics can be controlled as a group using All or None:
Diagnostics can be controlled independently:
Assume normality and symmetry but check for equal variances:
Unlisted assumptions are not tested:
The result is the same but a warning is issued:
Test assumption values can be explicitly set:
The sign test was previously chosen because the data is not normally distributed:
Bypassing diagnostic tests can save compute time:
It is often useful to bypass diagnostic tests for simulation purposes:
The assumptions of the test hold by design, so a great deal of time can be saved:
Applications (4)
Test whether the locations of some populations are equivalent:
The first two populations have similar locations:
The third population differs in location from the first:
The heart and body weights of a group of house cats were obtained:
The heart weight of male cats is significantly greater than that of female cats:
Perhaps male cats are just larger in general:
The ratio of heart weight to body weight is not significantly different between the sexes:
Six measurements were taken for 100 counterfeit Swiss banknotes and 100 genuine ones:
A plot of two of the measures for counterfeit and genuine notes:
A test of the bivariate median vectors shows a significant difference:
Samples were drawn from a pool of water at 10 randomly selected locations. Each sample was tested for zinc concentration at both the surface of the water and the bottom of the pool:
A visual inspection of the data. The distance between the vertical bars shows the quantity being tested under an assumption of dependence and independence respectively:
Assuming the data is paired yields a significant result not present under independence:
Assume a laboratory test showed that zinc concentrations form a gradient that becomes higher with increasing depth. This information justifies the use of a one-sided alternative:
Properties & Relations (9)
The ![]() -value suggests the expected proportion of false positives (Type I errors):
-value suggests the expected proportion of false positives (Type I errors):
Setting the size of a test to 0.05 results in an erroneous rejection of ![]() about 5% of the time:
about 5% of the time:
Type II errors arise when ![]() is not rejected, given it is false:
is not rejected, given it is false:
Increasing the size of the test lowers the Type II error rate:
The power of each test is the probability of rejecting ![]() when it is false:
when it is false:
The power of the tests at six different levels. The sign test has the lowest power in general:
The power of tests decreases with smaller sample sizes:
The power of the tests is lower than in the previous example:
For dependent samples, paired tests are more powerful than their non-paired counterparts:
Paired tests assume observations in one dataset are matched with observations in the other:
A paired ![]() -test is equivalent to a
-test is equivalent to a ![]() -test applied to the point-wise differences of two datasets:
-test applied to the point-wise differences of two datasets:
Paired tests assume that the data represents differences when given a single dataset:
A two-sided ![]() -value is twice the smaller of the two one-sided
-value is twice the smaller of the two one-sided ![]() -values:
-values:
The LocationTest works with the values only when the input is a TimeSeries:
LocationTest works with all the values together when the input is a TemporalData:
Test whether the means or medians of the two paths are equal:
Possible Issues (3)
Unknown variances and covariances are estimated from the data when using ![]() -type tests:
-type tests:
For large samples, the estimation has little effect on the results:
With small samples, ![]() -type tests should be used to account for the estimation:
-type tests should be used to account for the estimation:
Median-based tests should be used if the data is not normally distributed:
Median-based tests do not assume normality:
Changing the significance level affects internal diagnostics:
History
Text
Wolfram Research (2010), LocationTest, Wolfram Language function, https://reference.wolfram.com/language/ref/LocationTest.html.
CMS
Wolfram Language. 2010. "LocationTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/LocationTest.html.
APA
Wolfram Language. (2010). LocationTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LocationTest.html
BibTeX
@misc{reference.wolfram_2025_locationtest, author="Wolfram Research", title="{LocationTest}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/LocationTest.html}", note=[Accessed: 23-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_locationtest, organization={Wolfram Research}, title={LocationTest}, year={2010}, url={https://reference.wolfram.com/language/ref/LocationTest.html}, note=[Accessed: 23-February-2026]}