WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

MinimalPolynomial
✖
MinimalPolynomial

✖

gives the minimal polynomial in x for which the algebraic number s is a root.

✖

gives the minimal polynomial of the finite field element u over .

✖

gives the minimal polynomial of u over the -element subfield of the ambient field of u.

✖

gives the minimal polynomial of u relative to the finite field embedding emb.

Details and Options

  • MinimalPolynomial[s,x] gives the lowest-degree polynomial with integer coefficients, positive leading coefficient and the GCD of all coefficients equal to 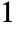for which the algebraic number s is a root.
  • MinimalPolynomial[s] gives a pure function representation of the minimal polynomial of s.
  • MinimalPolynomial[s,x,Extension->a] finds the characteristic polynomial of 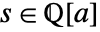over the field .
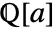  • For a FiniteFieldElement object u in a finite field 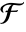of characteristic 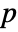, MinimalPolynomial[u, x] gives the lowest-degree monic polynomial with integer coefficients between 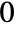and 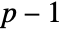for which u is a root.
  • MinimalPolynomial[u,x,k] gives the lowest-degree monic polynomial with coefficients from the 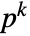-element subfield of 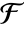for which u is a root. k needs to be a divisor of the extension degree of 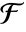over .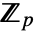
  • If emb=FiniteFieldEmbedding[e1e2], then MinimalPolynomial[u,x,emb] gives the polynomial with coefficients in the ambient field of e1 that map through emb to the coefficients of the minimal polynomial of u over the image of emb.

Examples

open allclose all

Basic Examples  (2)Summary of the most common use cases

Minimal polynomials of algebraic numbers:

In[1]:=1
✖
https://wolfram.com/xid/01yqbnyrdea-im1cws
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01yqbnyrdea-dob32q
Out[2]=2

Minimal polynomials of finite field elements:

In[1]:=1
✖
https://wolfram.com/xid/01yqbnyrdea-x0bw4
In[2]:=2
✖
https://wolfram.com/xid/01yqbnyrdea-bnly9d
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/01yqbnyrdea-jhf06g
Out[3]=3

Scope  (6)Survey of the scope of standard use cases

Algebraic Numbers  (5)

Radical expressions:

In[1]:=1
✖
https://wolfram.com/xid/01yqbnyrdea-mglz4c
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01yqbnyrdea-6aq8wg
Out[2]=2

Root objects:

In[1]:=1
✖
https://wolfram.com/xid/01yqbnyrdea-bg1khb
Out[1]=1

AlgebraicNumber objects:

In[1]:=1
✖
https://wolfram.com/xid/01yqbnyrdea-64kngp
Out[1]=1

MinimalPolynomial automatically threads over lists:

In[1]:=1
✖
https://wolfram.com/xid/01yqbnyrdea-o0e8qn
Out[1]=1

Pure function minimal polynomial:

In[1]:=1
✖
https://wolfram.com/xid/01yqbnyrdea-crxhkk
Out[1]=1

Finite Field Elements  (1)

Represent a finite field with characteristic and extension degree :

In[1]:=1
✖
https://wolfram.com/xid/01yqbnyrdea-o809yt
Out[1]=1

Minimal polynomial over :

In[2]:=2
✖
https://wolfram.com/xid/01yqbnyrdea-7hbsh
Out[2]=2

Minimal polynomial over with coefficients given as elements of :

In[3]:=3
✖
https://wolfram.com/xid/01yqbnyrdea-ib6kob
Out[3]=3

Minimal polynomial over the -element subfield of :

In[4]:=4
✖
https://wolfram.com/xid/01yqbnyrdea-j8qrez
Out[4]=4

Embed a field with elements in :

In[5]:=5
✖
https://wolfram.com/xid/01yqbnyrdea-441js
Out[6]=6

Minimal polynomial relative to the finite field embedding :

In[7]:=7
✖
https://wolfram.com/xid/01yqbnyrdea-m9l22y
Out[7]=7

Pure function minimal polynomial:

In[8]:=8
✖
https://wolfram.com/xid/01yqbnyrdea-yumhl
Out[8]=8

Options  (1)Common values & functionality for each option

Extension  (1)

Find the characteristic polynomial of over the extension TemplateBox[{}, Rationals][ⅇ^(ⅈ pi/4)] of :

In[1]:=1
✖
https://wolfram.com/xid/01yqbnyrdea-bsl4b4
Out[1]=1

The characteristic polynomial is a power of the minimal polynomial of :

In[2]:=2
✖
https://wolfram.com/xid/01yqbnyrdea-894mh
Out[2]=2

Applications  (3)Sample problems that can be solved with this function

Construct a polynomial with a root :

In[1]:=1
✖
https://wolfram.com/xid/01yqbnyrdea-pqp
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01yqbnyrdea-sma
Out[2]=2

The degree of the number field generated by (2-I)/Sqrt[5]:

In[1]:=1
✖
https://wolfram.com/xid/01yqbnyrdea-768nke
Out[1]=1

Check whether a finite field element generates its ambient field:

In[1]:=1
✖
https://wolfram.com/xid/01yqbnyrdea-ep9jbd
In[2]:=2
✖
https://wolfram.com/xid/01yqbnyrdea-fos1qn
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/01yqbnyrdea-q8yyvz
Out[3]=3

Properties & Relations  (6)Properties of the function, and connections to other functions

Compute the extension that defines the number field :

In[1]:=1
✖
https://wolfram.com/xid/01yqbnyrdea-djwm7c
Out[1]=1

Find the characteristic polynomial of over :

In[2]:=2
✖
https://wolfram.com/xid/01yqbnyrdea-prsinh
Out[2]=2

The characteristic polynomial is a power of the minimal polynomial of :

In[3]:=3
✖
https://wolfram.com/xid/01yqbnyrdea-le0ane
Out[3]=3

Use FrobeniusAutomorphism to find all conjugates of a finite field element a:

In[1]:=1
✖
https://wolfram.com/xid/01yqbnyrdea-carevw
Out[1]=1

The conjugates are roots of the minimal polynomial of a:

In[2]:=2
✖
https://wolfram.com/xid/01yqbnyrdea-bgtnzk
Out[2]=2

If MinimalPolynomial[a,x]xn+cn-1xn-1+⋯+c0, then :

In[1]:=1
✖
https://wolfram.com/xid/01yqbnyrdea-gdoney
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01yqbnyrdea-8ovzq
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/01yqbnyrdea-ig8hf
Out[3]=3

If MinimalPolynomial[a,x,k]xn+cn-1xn-1+⋯+c0, then :

In[1]:=1
✖
https://wolfram.com/xid/01yqbnyrdea-cjv48r
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01yqbnyrdea-o6cps4
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/01yqbnyrdea-dirv8
Out[3]=3

If MinimalPolynomial[a,x]xn+cn-1xn-1+⋯+c0, then :

In[1]:=1
✖
https://wolfram.com/xid/01yqbnyrdea-5x5hb
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01yqbnyrdea-b7s0kw
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/01yqbnyrdea-c3g488
Out[3]=3

If MinimalPolynomial[a,x,k]xn+cn-1xn-1+⋯+c0, then :

In[1]:=1
✖
https://wolfram.com/xid/01yqbnyrdea-es2w9k
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/01yqbnyrdea-ga3ozb
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/01yqbnyrdea-u2geu
Out[3]=3
Wolfram Research (2007), MinimalPolynomial, Wolfram Language function, https://reference.wolfram.com/language/ref/MinimalPolynomial.html (updated 2023).
✖
Wolfram Research (2007), MinimalPolynomial, Wolfram Language function, https://reference.wolfram.com/language/ref/MinimalPolynomial.html (updated 2023).

Text

Wolfram Research (2007), MinimalPolynomial, Wolfram Language function, https://reference.wolfram.com/language/ref/MinimalPolynomial.html (updated 2023).

✖
Wolfram Research (2007), MinimalPolynomial, Wolfram Language function, https://reference.wolfram.com/language/ref/MinimalPolynomial.html (updated 2023).

CMS

Wolfram Language. 2007. "MinimalPolynomial." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/MinimalPolynomial.html.

✖
Wolfram Language. 2007. "MinimalPolynomial." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/ref/MinimalPolynomial.html.

APA

Wolfram Language. (2007). MinimalPolynomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MinimalPolynomial.html

✖
Wolfram Language. (2007). MinimalPolynomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MinimalPolynomial.html

BibTeX

@misc{reference.wolfram_2025_minimalpolynomial, author="Wolfram Research", title="{MinimalPolynomial}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/MinimalPolynomial.html}", note=[Accessed: 06-April-2025 ]}

✖
@misc{reference.wolfram_2025_minimalpolynomial, author="Wolfram Research", title="{MinimalPolynomial}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/MinimalPolynomial.html}", note=[Accessed: 06-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_minimalpolynomial, organization={Wolfram Research}, title={MinimalPolynomial}, year={2023}, url={https://reference.wolfram.com/language/ref/MinimalPolynomial.html}, note=[Accessed: 06-April-2025 ]}

✖
@online{reference.wolfram_2025_minimalpolynomial, organization={Wolfram Research}, title={MinimalPolynomial}, year={2023}, url={https://reference.wolfram.com/language/ref/MinimalPolynomial.html}, note=[Accessed: 06-April-2025 ]}