BUILT-IN MATHEMATICA SYMBOL

MomentGeneratingFunction

gives the moment generating function for the symbolic distribution dist as a function of the variable t.

gives the moment generating function for the multivariate symbolic distribution dist as a function of the variables

,

, ....

MORE INFORMATION

MomentGeneratingFunction is equivalent to Expectation[Exp[t x], xdist].

MomentGeneratingFunction is equivalent to Expectation[Exp[t.x], xdist] for vectors t and x.

The i 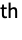moment can be extracted from a moment generating function mgf through SeriesCoefficient[mgf, {t, 0, i}]i!.

EXAMPLES

CLOSE ALL

Basic Examples (3)

Compute the moment generating function (mgf) for a continuous univariate distribution:

The mgf for a univariate discrete distribution:

The mgf for a multivariate distribution:

Compute the moment generating function (mgf) for a continuous univariate distribution:

In[1]:=

Out[1]=

The mgf for a univariate discrete distribution:

In[1]:=

Out[1]=

The mgf for a multivariate distribution:

In[1]:=

Out[1]=

Scope (4)

Compute the moment generating function (mgf) for a formula distribution:

Find the mgf for a function of a random variate:

Find the mgf for a data distribution:

Compute the mgf for a censored distribution:

Applications (3)

Find the moment generating function of the sum of random variates:

Check that it is equal to the product of generating functions:

When

it coincides with the mgf of BinomialDistribution:

Confirm with TransformedDistribution:

Reconstruct the PDF of a positive real random variate from its moment generating function:

Check the result:

Illustrate the central limit theorem on the example of PoissonDistribution:

Find the moment generating function for the standardized random variate:

Find the moment generating function for the sum of

standardized random variates rescaled by

:

Find the large

limit:

Compare with the moment generating function of standard normal distribution:

Properties & Relations (5)

MomentGeneratingFunction is equivalent to Expectation of

:

MomentGeneratingFunction is an exponential generating function for the sequence of moments:

Use SeriesCoefficient to find moment

:

Use Moment directly:

MomentGeneratingFunction is a LaplaceTransform for positive random variables:

MomentGeneratingFunction is a ZTransform for discrete positive random variates:

Possible Issues (2)

For some distributions with long tails, moments of only several low orders are defined:

Correspondingly, MomentGeneratingFunction is undefined:

Analytic continuation of CharacteristicFunction can sometimes be defined:

MomentGeneratingFunction is not always known in closed form:

Use Moment to evaluate particular moments:

Neat Examples (1)