 |
BUILT-IN MATHEMATICA SYMBOL
Piecewise
Piecewise[{{val1, cond1}, {val2, cond2}, ...}]
represents a piecewise function with values 
in the regions defined by the conditions 
.
Piecewise[{{val1, cond1}, ...}, val]
uses default value val if none of the 
apply. The default for val is 
.
Details
- The
are typically inequalities such as 
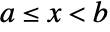. - The
are evaluated in turn, until one of them is found to yield True. - If all preceding
yield False, then the 
corresponding to the first 
that yields True is returned as the value of the piecewise function. - If any of the preceding
do not literally yield False, the Piecewise function is returned in symbolic form. - Only those
explicitly included in the returned form are evaluated. - Elements of the form {vali, False} are dropped, as are all elements after the first {vali, True}.
- Piecewise[conds] automatically evaluates to Piecewise[conds, 0].
- Piecewise can be used in such functions as Integrate, Minimize, Reduce, DSolve, and Simplify, as well as their numeric analogs.
- Piecewise[{{v1, c1}, {v2, c2}, ...}] can be input in the form
. The piecewise operator 
can be entered as EscpwEsc or \[Piecewise]. The grid of values and conditions can be constructed by first entering Ctrl+Comma, then using Ctrl+![DynamicBox[ToBoxes[If[$OperatingSystem === MacOSX, Return, Enter], StandardForm], ImageSizeCache -> {39., {0., 9.}}]](Files/Piecewise.en/15.png "DynamicBox[ToBoxes[If[$OperatingSystem === MacOSX, Return, Enter], StandardForm], ImageSizeCache -> {39., {0., 9.}}]")
and Ctrl+Comma. - In StandardForm and TraditionalForm, Piecewise[{{v1, c1}, {v2, c2}, ...}] is normally output using a brace, as in
.
![Ctrl+DynamicBox[ToBoxes[If[$OperatingSystem === MacOSX, Return, Enter], StandardForm], ImageSizeCache -> {30., {0., 8.}}]](Files/Piecewise.en/18.png "Ctrl+DynamicBox[ToBoxes[If[$OperatingSystem === MacOSX, Return, Enter], StandardForm], ImageSizeCache -> {30., {0., 8.}}]"){kind=small}
New in 5.1
