

RankedMax
Details
- RankedMax yields a definite result if all its arguments are real numbers.
- If
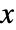 is a list with the ordering
is a list with the ordering  , then RankedMax[x,n] gives
, then RankedMax[x,n] gives 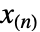 and RankedMax[x,-n] gives
and RankedMax[x,-n] gives 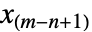 for
for 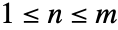 .
. - RankedMax[{x1,…,xm},1] is equivalent to Max[{x1,…,xm}]. »
- RankedMax[{x1,…,xm},-1] is equivalent to Min[{x1,…,xm}].
- RankedMax[{x1,…,xm},m] is equivalent to Min[{x1,…,xm}]. »
- RankedMax[{x1,…,xm},n] is equivalent to Quantile[{x1,…,xm},(m-n+1)/m]. »
Examples
open all close allBasic Examples (4)
Scope (25)
Numerical Evaluation (7)
Evaluate the second largest of three numbers:
The fourth largest—i.e the smallest—of four numbers:
The second smallest of five numbers:
The fourth smallest of five numbers:
The fifth smallest—i.e. the largest—of five numbers:
Evaluate efficiently at high precision:
RankedMax of WeightedData ignores the weights:
Specific Values (4)
Solve equations and inequalities:
Find a value of x for which RankedMax[{Sin[x],Cos[x],Exp[x]},2]1:
Visualization (3)
Function Properties (8)
RankedMax is only defined for real-valued inputs:
The range of RankedMax is real numbers:
Basic symbolic simplification is done automatically:
Multi-argument ranked RankedMax is generally not an analytic function:
It will have singularities where the functions cross, but it will be continuous:
Applications (7)
Plot the bivariate RankedMax functions:
Plot the contours of bivariate and trivariate RankedMax functions:
RankedMax[{y1,…,yn,x},k] as a function of x:
Compute the expectation of the second smallest (median) variable:
Alternatively, use OrderDistribution:
Compute the probability of the second smallest variable being less than 1:
Find the height of the fourth tallest child in a class:
Properties & Relations (6)
RankedMax[{x1,…,xm},1] is equivalent to Max[x1,…,xm]:
RankedMax[{x1,…,xm},m] is equivalent to Min[x1,…,xm]:
RankedMax[{x1,…,xm},k] is equivalent to RankedMin[{x1,…,xm},m-k+1]:
RankedMax[{x1,…,xm},n] is equivalent to Quantile[{x1,…,xm},(m-n+1)/m]:
RankedMax[{x1,…,xm},n] is equivalent to Sort[{x1,…,xm},Greater]〚n〛:
The equivalent Piecewise function has disjoint piecewise case domains:
Algebraically prove the piecewise case domains are disjoint:
Algebraically prove the piecewise case domains are pairwise disjoint:
Related Guides
Text
Wolfram Research (2010), RankedMax, Wolfram Language function, https://reference.wolfram.com/language/ref/RankedMax.html (updated 2024).
CMS
Wolfram Language. 2010. "RankedMax." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/RankedMax.html.
APA
Wolfram Language. (2010). RankedMax. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RankedMax.html
BibTeX
@misc{reference.wolfram_2025_rankedmax, author="Wolfram Research", title="{RankedMax}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/RankedMax.html}", note=[Accessed: 25-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_rankedmax, organization={Wolfram Research}, title={RankedMax}, year={2024}, url={https://reference.wolfram.com/language/ref/RankedMax.html}, note=[Accessed: 25-February-2026]}