Rotate

Rotate[g,θ]

represents 2D graphics primitives or any other objects g rotated counterclockwise by θ radians about the center of their bounding box.

Rotate[g,θ,{x,y}]

rotates about the point {x,y}.

Rotate[g,{u,v}]

rotates around the origin, transforming the 2D or 3D vector u to v.

Rotate[g,θ,w]

rotates 3D graphics primitives by θ radians around the 3D vector w anchored at the origin.

Rotate[g,θ,w,p]

rotates around the 3D vector w anchored at p.

Rotate[g,θ,{u,v}]

rotates by angle θ in the plane spanned by 3D vectors u and v.

Details and Options

  • θ Degree or θ° specifies an angle in degrees.
  • If Rotate appears outside a graphic, the object g in Rotate[g,θ] etc. can be any expression.
  • You can specify special points such as {Left,Bottom} within the bounding box for g.
  • The x position can be specified as Left, Center, or Right; the y position as Bottom, Center, or Top.
  • If Rotate appears within a graphic, the coordinates {x,y} are taken to be in the coordinate system of the graphic.
  • If Rotate appears outside a graphic, the coordinates {x,y} are taken to run from 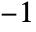to 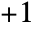across the bounding box of the object being rotated.
  • Rotate[g,θ] is equivalent to Rotate[g,θ,{Center,Center}].
  • For objects specified with scaled coordinates Scaled[{x,y}], Rotate effectively applies its transformation to the corresponding ordinary coordinates.
  • If Rotate appears inside a graphic, Normal[expr] if possible replaces all Rotate[gi,…] constructs by versions of the gi in which the coordinates have explicitly been transformed.

Examples

open allclose all

Basic Examples  (3)

Rotate a square by 30°:

Rotate a cuboid by 30° around the axis:

Rotate text by 45°:

Scope  (8)

Transformation applied to a 2D shape:

Transformation applied to a 3D shape:

Rotation around the vector anchored at the point :

Rotation mapping vector to vector :

Rotation in the plane spanned by vectors and :

Rotate text:

Rotate objects with scaled coordinates:

Keep the lower-right corner of the rectangle fixed:

Applications  (2)

Grid with vertical text:

Diamond grid:

Properties & Relations  (1)

When possible, Normal will transform the coordinates explicitly:

Possible Issues  (4)

By default, Rotate uses the center of the bounding box as the center of rotation:

Explicitly specify a center of rotation:

Transforming an object may move it out of view:

Adjust the PlotRange to display the transformed object:

The center of the baseline of rotated text aligns with the baseline of the surrounding text:

For a different alignment, specify an explicit center of rotation:

Since text bounding boxes are always rectilinear, successive rotations can introduce extra space:

Neat Examples  (2)

Rotations of a regular polygon:

Nested, rotated square roots:

Wolfram Research (2007), Rotate, Wolfram Language function, https://reference.wolfram.com/language/ref/Rotate.html (updated 2008).

Text

Wolfram Research (2007), Rotate, Wolfram Language function, https://reference.wolfram.com/language/ref/Rotate.html (updated 2008).

CMS

Wolfram Language. 2007. "Rotate." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2008. https://reference.wolfram.com/language/ref/Rotate.html.

APA

Wolfram Language. (2007). Rotate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Rotate.html

BibTeX

@misc{reference.wolfram_2024_rotate, author="Wolfram Research", title="{Rotate}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/Rotate.html}", note=[Accessed: 30-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_rotate, organization={Wolfram Research}, title={Rotate}, year={2008}, url={https://reference.wolfram.com/language/ref/Rotate.html}, note=[Accessed: 30-December-2024 ]}