- See Also
-
Related Guides
- Descriptive Statistics
- Time Series Processing
- Statistical Data Analysis
- Statistical Moments and Generating Functions
- GPU Computing
- Using the Wolfram Data Drop
- Numbers with Uncertainty
- Date & Time
- Tabular Modeling
- GPU Computing with Apple
- GPU Computing with NVIDIA
- Probability & Statistics with Quantities
- Tabular Transformation
- Symbolic Vectors, Matrices and Arrays
- Tech Notes
-
- See Also
-
Related Guides
- Descriptive Statistics
- Time Series Processing
- Statistical Data Analysis
- Statistical Moments and Generating Functions
- GPU Computing
- Using the Wolfram Data Drop
- Numbers with Uncertainty
- Date & Time
- Tabular Modeling
- GPU Computing with Apple
- GPU Computing with NVIDIA
- Probability & Statistics with Quantities
- Tabular Transformation
- Symbolic Vectors, Matrices and Arrays
- Tech Notes
StandardDeviation[data]
gives the standard deviation estimate of the elements in data.
StandardDeviation[dist]
gives the standard deviation of the distribution dist.


StandardDeviation
StandardDeviation[data]
gives the standard deviation estimate of the elements in data.
StandardDeviation[dist]
gives the standard deviation of the distribution dist.
Details




- StandardDeviation is also known as volatility.
- StandardDeviation measures dispersion from the mean of data or distributions.
- For VectorQ data
 with
with 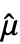 =Mean[data], the standard deviation estimate
=Mean[data], the standard deviation estimate 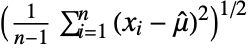 is given by
is given by 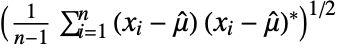 for reals and
for reals and 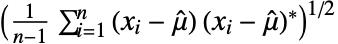 for complexes.
for complexes. - For MatrixQ data, the standard deviation estimate
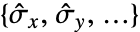 is computed for each column vector with StandardDeviation[{{x1,y1,…},{x2,y2,…},…}] equivalent to {StandardDeviation[{x1,x2,…}],StandardDeviation[{y1,y2,…}]}. »
is computed for each column vector with StandardDeviation[{{x1,y1,…},{x2,y2,…},…}] equivalent to {StandardDeviation[{x1,x2,…}],StandardDeviation[{y1,y2,…}]}. » - For ArrayQ data, standard deviation is equivalent to ArrayReduce[StandardDeviation,data,1]. »
- For a real weighted WeightedData[{x1,x2,…},{w1,w2,…}], the standard deviation is given by
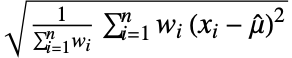 . »
. » - StandardDeviation handles both numerical and symbolic data.
- The data can have the following additional forms and interpretations:
-
Association the values (the keys are ignored) » SparseArray as an array, equivalent to Normal[data] » QuantityArray quantities as an array » WeightedData weighted variance, based on the underlying EmpiricalDistribution » EventData based on the underlying SurvivalDistribution » TimeSeries, TemporalData, … vector or array of values (the time stamps ignored) » Image,Image3D RGB channel's values or grayscale intensity value » Audio amplitude values of all channels » DateObject, TimeObject list of dates or list of times » - For a univariate distribution dist, the standard deviation is given by σ=Expectation[(x-μ)2,xdist]1/2 with μ=Mean[dist]. »
- For multivariate distribution dist, the standard deviation is given by {σx,σy,…}=Expectation[{(x-μx)2,(y-μy)2,…},{x,y,…}dist]1/2. »
- For a random process proc, the standard deviation function
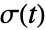 can be computed for slice distribution at time t, SliceDistribution[proc,t], as σ[t]=StandardDeviation[SliceDistribution[proc,t]]. »
can be computed for slice distribution at time t, SliceDistribution[proc,t], as σ[t]=StandardDeviation[SliceDistribution[proc,t]]. »
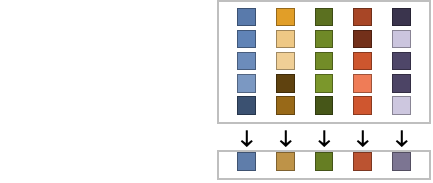
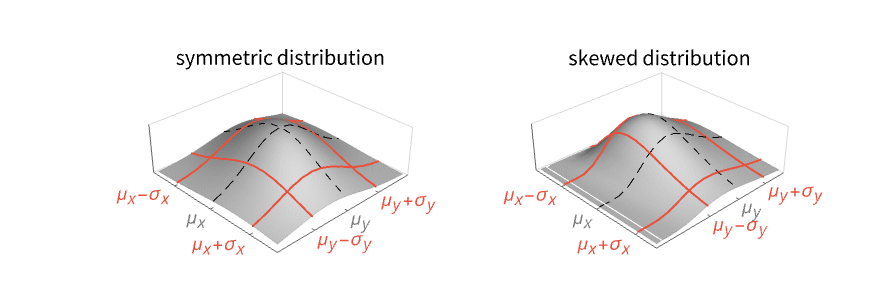
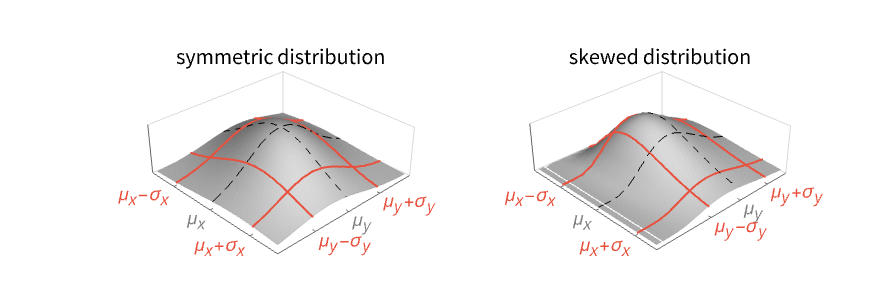
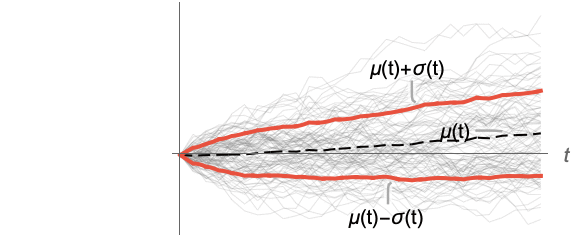
Examples
open all close allBasic Examples (4)
Scope (24)
Basic Uses (8)
Exact input yields exact output:
Approximate input yields approximate output:
Find the standard deviation of WeightedData:
Find the standard deviation of EventData:
Find the standard deviation of TemporalData:
Find the standard deviation of a TimeSeries:
The standard deviation depends only on the values:
Array Data (5)
StandardDeviation for a matrix gives columnwise standard deviations:
StandardDeviation for a tensor gives columnwise standard deviations at the first level:
When the input is an Association, StandardDeviation works on its values:
SparseArray data can be used just like dense arrays:
Find the standard deviation of a QuantityArray:
Image and Audio Data (2)
Channelwise standard deviation of an RGB image:
Standard deviation of a grayscale image:
On audio objects, StandardDeviation works channelwise:
Date and Time (5)
Applications (7)
StandardDeviation is a measure of dispersion:
Transform data to have mean 0 and unit variance:
Identify periods of high volatility in the S&P 500 using a five-year moving standard deviation:
Find the mean and standard deviation for the number of cycles to failure of deep-groove ball-bearings:
Probability that the values lie within two standard deviations of the mean:
Investigate weak stationarity of the process data by analyzing standard deviations of slices:
Use a larger plot range to see how relatively small the variations are:
Compute standard deviation for slices of a collection of paths of a random process:
Compute standard deviations and means:
Create a standard deviation band around the mean:
Plot standard deviations around the mean over these paths:
Find the standard deviation of the heights for the children in a class:
Properties & Relations (9)
The square of StandardDeviation is Variance:
StandardDeviation is a scaled Norm of deviations from the Mean:
StandardDeviation is the square root of a scaled CentralMoment:
StandardDeviation is a scaled RootMeanSquare of the deviations:
StandardDeviation is the square root of a scaled Mean of squared deviations:
StandardDeviation as a scaled EuclideanDistance from the Mean:
StandardDeviation squared is less than MeanDeviation if all absolute deviations are less than 1:
StandardDeviation squared is greater than MeanDeviation if all absolute deviations are greater than 1:
StandardDeviation of a random variable as the square root of Variance:
Neat Examples (1)
The distribution of StandardDeviation estimates for 20, 100, and 300 samples:
See Also
Variance Mean MeanDeviation MedianDeviation TrimmedVariance WinsorizedVariance BiweightMidvariance QnDispersion SnDispersion Kurtosis CentralMoment Covariance MeanAround Standardize StandardDeviationFilter Expectation Quantile
Function Repository: PopulationStandardDeviation PooledStandardDeviation PopulationVariance StatisticsSummary StudentTValue
Tech Notes
Related Guides
-
▪
- Descriptive Statistics ▪
- Time Series Processing ▪
- Statistical Data Analysis ▪
- Statistical Moments and Generating Functions ▪
- GPU Computing ▪
- Using the Wolfram Data Drop ▪
- Numbers with Uncertainty ▪
- Date & Time ▪
- Tabular Modeling ▪
- GPU Computing with Apple ▪
- GPU Computing with NVIDIA ▪
- Probability & Statistics with Quantities ▪
- Tabular Transformation ▪
- Symbolic Vectors, Matrices and Arrays
History
Introduced in 2003 (5.0) | Updated in 2007 (6.0) ▪ 2023 (13.3) ▪ 2024 (14.1)
Text
Wolfram Research (2003), StandardDeviation, Wolfram Language function, https://reference.wolfram.com/language/ref/StandardDeviation.html (updated 2024).
CMS
Wolfram Language. 2003. "StandardDeviation." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/StandardDeviation.html.
APA
Wolfram Language. (2003). StandardDeviation. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StandardDeviation.html
BibTeX
@misc{reference.wolfram_2025_standarddeviation, author="Wolfram Research", title="{StandardDeviation}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/StandardDeviation.html}", note=[Accessed: 04-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_standarddeviation, organization={Wolfram Research}, title={StandardDeviation}, year={2024}, url={https://reference.wolfram.com/language/ref/StandardDeviation.html}, note=[Accessed: 04-March-2026]}