 |
BUILT-IN MATHEMATICA SYMBOL
StirlingS2
StirlingS2[n, m]
gives the Stirling number of the second kind 
.
Details
- Integer mathematical function, suitable for both symbolic and numerical manipulation.
gives the number of ways of partitioning a set of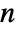 
elements into 
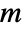non-empty subsets. - StirlingS2 automatically threads over lists.
New in 1
