x^y
gives ![]() to the power
to the power ![]() .
.




Power 
x^y
gives ![]() to the power
to the power ![]() .
.
Details

- Mathematical function, suitable for both symbolic and numerical manipulation.
- Exact rational number results are given when possible for roots of the form
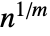 .
. - For complex numbers
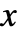 and
and 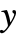 , Power gives the principal value of
, Power gives the principal value of 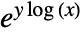 . »
. » 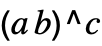 is automatically converted to
is automatically converted to 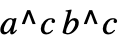 only if
only if 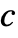 is an integer.
is an integer. 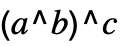 is automatically converted to
is automatically converted to 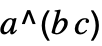 only if
only if 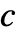 is an integer.
is an integer. - For certain special arguments, Power automatically evaluates to exact values.
- Power can be evaluated to arbitrary numerical precision.
- Power automatically threads over lists.
- Power[x,y] has a branch cut discontinuity for noninteger
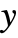 running from
running from 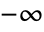 to 0 in the complex
to 0 in the complex 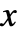 plane.
plane. - Power[x,y,z,…] is taken to be Power[x,Power[y,z,…]].
- Power can be used with Interval and CenteredInterval objects. »
Background & Context
- Power is a mathematical function that raises an expression to a given power. The expression Power[x,y] is commonly represented using the shorthand syntax x^y or written in 2D typeset form as xy. A number to the first power is equal to itself (
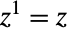 ), and 1 to any complex power is equal to 1 (
), and 1 to any complex power is equal to 1 (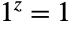 ). The inverse of a power function is given by Log, so solving the equation
). The inverse of a power function is given by Log, so solving the equation 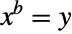 for
for 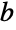 gives a principal solution of
gives a principal solution of 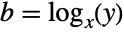 .
. - The operation of taking an expression to the second power is known as “squaring” and the operation of taking an expression to the third power is known as “cubing”. The rules for combining quantities containing powers are called the exponent laws, and the process of raising a base to a given power is known as exponentiation. Many expressions involving Power, Exp, Log, and related functions are automatically simplified or else may be simplified using Simplify or FullSimplify. PowerExpand can be used to do formal expansion and associated simplification, and ExpToTrig can be used to get trigonometric forms of Power expressions.
- The function Sqrt[x] is represented using Power[x,1/2]. Exponentiation using the base of the natural logarithm E can be input as Exp[x] but is represented using Power[E,x].
- Power[x,y] has a branch cut discontinuity for y running from
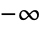 to 0 in the complex x plane for noninteger y. Because of this branch cut, Power[x,1/n] returns a complex root by default instead of the real one for negative real x and odd positive n. To obtain a real-valued n
to 0 in the complex x plane for noninteger y. Because of this branch cut, Power[x,1/n] returns a complex root by default instead of the real one for negative real x and odd positive n. To obtain a real-valued n root, Surd[x,n] can be used. The special case CubeRoot[x] corresponds to Surd[x,3].
root, Surd[x,n] can be used. The special case CubeRoot[x] corresponds to Surd[x,3].
Examples
open all close allBasic Examples (6)
Enter as a superscript using ![]() :
:
Explicit FullForm:
Plot over a subset of the reals:
Scope (46)
Numerical Evaluation (9)
Efficiently compute the first million digits of a result:
Complex numbers are generated when necessary:
The principal root is always used:
This follows from the general definition of Power as ![]() :
:
Surd can be used to get the real root:
Power threads elementwise over lists and matrices:
Power can be used with Interval and CenteredInterval objects:
Compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix Power function using MatrixFunction:
Specific Values (4)
Depending on the real part of ![]() , the result can be 0 or infinity:
, the result can be 0 or infinity:
Hence the following is indeterminate:
Find a value of x for which the Power[x,3]=0.5:
Visualization (5)
Function Properties (11)
![]() is defined for all real
is defined for all real ![]() when
when ![]() :
:
It is only defined for integer ![]() when
when ![]() :
:
For nonzero complex ![]() , it is an entire function of
, it is an entire function of ![]() :
:
Power is right-associative:
The form on the right-hand side is the preferred form:
Power is periodic in its second argument in the complex plane:
For fixed, positive integer ![]() ,
, ![]() is an analytic function of
is an analytic function of ![]() :
:
It is not analytic, but it is still meromorphic for negative integers ![]() :
:
For noninteger ![]() , it is not even meromorphic:
, it is not even meromorphic:
For a fixed, nonzero real ![]() ,
, ![]() is an analytic function of
is an analytic function of ![]() :
:
As a bivariate function, ![]() is neither analytic nor meromorphic:
is neither analytic nor meromorphic:
![]() is not surjective onto the reals for any value of
is not surjective onto the reals for any value of ![]() :
:
![]() has in general singularities for
has in general singularities for ![]() or for
or for ![]() :
:
Differentiation (4)
Integration (3)
Compute the indefinite integral using Integrate:
Series Expansions (4)
Find the Taylor expansion using Series:
Plots of the first three approximations around ![]() :
:
General term in the series expansion using SeriesCoefficient:
Function Identities and Simplifications (6)
Connection with Exp function:
Nested powers are not always automatically combined:
Use PowerExpand to force cancellation:
This can produce incorrect results:
Alternatively, use Simplify with appropriate assumptions:
Applications (5)
Find the radius of a sphere of the same volume as a cube with side ![]() :
:
Contour plot of a complex inverse power:
Find integrals of rational functions in terms of Log:
Solve a differential equation with variable rational coefficients:
Properties & Relations (27)
Equivalent forms for square roots:
Whole powers of roots are automatically simplified:
Roots of powers cannot be automatically simplified:
Use Power[x,1/n] or ![]() to find the principle complex root:
to find the principle complex root:
Use Surd[x,n] to find the nth real root:
Use PowerExpand to do formal simplification:
Get results valid for all complex ![]() :
:
Use ExpToTrig to get trigonometric forms:
Use Solve or Root to find all roots:
Use Expand to expand out powers of polynomials:
Powers are automatically applied to series:
Equations involving powers can have infinitely many solutions:
Reciprocals, square roots, etc. are automatically converted to powers:
Exponentials are converted to powers:
Branch cut structure for fractional powers in the complex plane:
Test whether powers are algebraic:
Power appears in special cases of many mathematical functions:
Power can be represented as a DifferenceRoot:
General term in the series expansion of Power:
The generating function for Power:
FindSequenceFunction can recognize the Power sequence:
The exponential generating function for Power:
Use GeneralizedPower to represent an integer power of an arbitrary binary operation:
Power is GeneralizedPower of Times:
Possible Issues (13)
Power always computes principal roots:
Powers are not generically inverses of roots:
With approximate numbers, imaginary parts can be generated:
Use Chop to remove the small imaginary part:
The branch cut makes this function discontinuous:
Its derivative nevertheless generically gives 0:
Machine precision can give incorrect numerical results on the branch cut:
Machine-number inputs can give arbitrary-precision results:
Some powers are too large for any computer:
Powers can give indeterminate expressions:
The precision of each result is determined by the precision of the zero:
Symbolic powers of 1 are only evaluated when the 1 is an exact or machine-precision number:
Numerical decision procedures with default settings cannot simplify this power:
Machine-precision numerical evaluation is inadequate:
Higher internal precision resolves the result:
Nonrational powers are not absorbed into series:
Power applies elementwise to matrices:
Use MatrixPower for matrix powers:
Tech Notes
Related Guides
History
Introduced in 1988 (1.0) | Updated in 2021 (13.0)
Text
Wolfram Research (1988), Power, Wolfram Language function, https://reference.wolfram.com/language/ref/Power.html (updated 2021).
CMS
Wolfram Language. 1988. "Power." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/Power.html.
APA
Wolfram Language. (1988). Power. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Power.html
BibTeX
@misc{reference.wolfram_2025_power, author="Wolfram Research", title="{Power}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Power.html}", note=[Accessed: 07-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_power, organization={Wolfram Research}, title={Power}, year={2021}, url={https://reference.wolfram.com/language/ref/Power.html}, note=[Accessed: 07-February-2026]}