 |
BUILT-IN MATHEMATICA SYMBOL
TensorWedge 
TensorWedge[tensor1, tensor2, ...]
represents the antisymmetrized tensor product of the 
.
Details
- TensorWedge[a, b] can be input as
. The character 
is entered as Esct^Esc or \[TensorWedge]. - In a tensor wedge product of explicit or symbolic arrays, all slots must have the same dimension
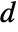, though different arrays may have different ranks. TensorWedge generalizes Cross, which requires 
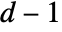vectors of length 
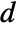. - The TensorWedge product of several arrays is an antisymmetric array, always given in SymmetrizedArray form.
- If the tensors
are not antisymmetric, then they are effectively antisymmetrized before performing the product. Vectors are considered antisymmetric tensors of rank 1. Scalars are considered antisymmetric tensors of rank 0. - The wedge product TensorWedge[t1, ..., tk] of the antisymmetric tensors
is equivalent to Multinomial[r1, ..., rk]*Symmetrize[TensorProduct[t1, ..., tk], Antisymmetric[All]], where 
is the tensor rank of 
.
New in 9
