"ImplicitRungeKutta" Method for NDSolve
Introduction
Implicit Runge-Kutta methods have a number of desirable properties.
The Gauss-Legendre methods, for example, are self-adjoint, meaning that they provide the same solution when integrating forward or backward in time.
This loads packages defining some example problems and utility functions.
Coefficients
A generic framework for implicit Runge-Kutta methods has been implemented. The focus so far is on methods with interesting geometric properties and currently covers the following schemes:
Coefficient Generation
- Start with the definition of the polynomial, defining the abscissas of the
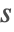stage coefficients. For example, the abscissas for Gauss-Legendre methods are defined as 
.
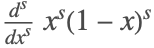- Univariate polynomial factorization gives the underlying irreducible polynomials defining the roots of the polynomials.
- Root objects are constructed to represent the solutions (using unique root isolation and Jenkins-Traub for the numerical approximation).
- Root objects are then approximated numerically for precision coefficients.
- Condition estimates for Vandermonde systems governing the coefficients yield the precision to take in approximating the roots numerically.
- Specialized solvers for nonconfluent Vandermonde systems are then used to solve equations for the coefficients (see [GVL96]).
- One step of iterative refinement is used to polish the approximate solutions and to check that the coefficients are obtained to the requested precision.
This generates the coefficients for the two-stage fourth-order Gauss-Legendre method to 50 decimal digits of precision.
| Out[5]= |  |
The coefficients have the form
.
This generates the coefficients for the two-stage fourth-order Gauss-Legendre method exactly. For high-order methods, generating the coefficients exactly can often take a very long time.
| Out[6]= |  |
This generates the coefficients for the six-stage tenth-order RaduaIA implicit Runge-Kutta method to 20 decimal digits of precision.
| Out[7]= |  |
Examples
This problem has two invariants that should remain constant. A numerical method may not be able to conserve these invariants.
| Out[10]= |  |
This solves the system using an implicit Runge-Kutta Gauss method. The order of the scheme is selected using the
method option.
| Out[11]= |  |
A plot of the error in the invariants shows an increase as the integration proceeds.
| Out[12]= |  |
The
method of
has options
AccuracyGoal and
PrecisionGoal that specify the absolute and relative error to aim for in solving the nonlinear system of equations.
These options have the same default values as the corresponding options in
NDSolve, since often there is little point in solving the nonlinear system to much higher accuracy than the local error of the method.
However, for certain types of problems it can be useful to solve the nonlinear system up to the working precision.
| Out[13]= |  |
The first invariant is the Hamiltonian of the system, and the error is now bounded, as it should be, since the Gauss implicit Runge-Kutta method is a symplectic integrator.
The second invariant is conserved exactly (up to roundoff) since the Gauss implicit Runge-Kutta method conserves quadratic invariants.
| Out[14]= |  |
This defines the implicit midpoint method as the one-stage implicit Runge-Kutta method of order two.
For this problem it can be more efficient to use a fixed-point iteration instead of a Newton iteration to solve the nonlinear system.
| Out[16]= |  |
At present, the implicit Runge-Kutta method framework does not use banded Newton techniques for uncoupling the nonlinear system.
Option Summary
"ImplicitRungeKutta" Options
| | |
| "Coefficients" | "ImplicitRungeKuttaGaussCoefficients" | specify the coefficients to use in the implicit Runge-Kutta method |
| "DifferenceOrder" | Automatic | specify the order of local accuracy of the method |
| "ImplicitSolver" | "Newton" | specify the solver to use for the nonlinear system; valid settings are FixedPoint or  |
| "StepSizeControlParameters" | Automatic | specify the step control parameters |
| "StepSizeRatioBounds" | { ,4} | specify the bounds on a relative change in the new step size |
| "StepSizeSafetyFactors" | Automatic | specify the safety factors to use in the step size estimate |
Options of the method 
.
The default setting of
Automatic for the option
uses the values
.
"ImplicitSolver" Options
| | |
| AccuracyGoal | Automatic | specify the absolute tolerance to use in solving the nonlinear system |
| "IterationSafetyFactor" |  | specify the safety factor to use in solving the nonlinear system |
| MaxIterations | Automatic | specify the maximum number of iterations to use in solving the nonlinear system |
| PrecisionGoal | Automatic | specify the relative tolerance to use in solving the nonlinear system |
Common options of 
.
| | |
| "JacobianEvaluationParameter" |  | specify when to recompute the Jacobian matrix in Newton iterations |
| "LinearSolveMethod" | Automatic | specify the linear solver to use in Newton iterations |
| "LUDecompositionEvaluationParameter" |  | specify when to compute LU decompositions in Newton iterations |
Options specific to the 
method of 
.
