WSMLink`
WSMLink`

WSMSimulateSensitivity

WSMSimulateSensitivity is being phased out in favor of SystemModelSimulateSensitivity, which was introduced experimentally in Version 11.3.

WSMSimulateSensitivity["mmodel",{p1,p2,…}]

simulates "mmodel" and sensitivities to parameters pi following experiment settings.

WSMSimulateSensitivity["mmodel",tmax,{p1,p2,…}]

simulates from 0 to tmax.

WSMSimulateSensitivity["mmodel",{tmin,tmax},{p1,p2,…}]

simulates from tmin to tmax.

WSMSimulateSensitivity["mmodel",vars,{tmin,tmax},{p1,p2,…}]

stores only simulation data for the variables vars.

Details and Options

  • WSMSimulateSensitivity returns a WSMSimulationData object.
  • The "mmodel" refers to the fully qualified Modelica name.
  • WSMSimulateSensitivity generates solutions 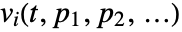for all variables 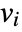, as well as derivatives 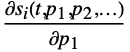, , 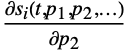… for all states 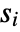, for .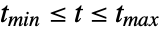
  • Sensitivities can be listed in a WSMSimulationData object sd with sd["SensitivityNames"].
  • The shortest unique model name mmodel can be used where WSMNames["*.mmodel"] gives a unique match.
  • The stored simulation variables vars can have the following values:
  • Automaticautomatically choose what to store
    {v1,v2,…}store only variables vi
    Allstore all variables
  • The following options can be given:
  • InterpolationOrderAutomaticcontinuity degree of output between events
    WSMInitialValuesAutomaticoverriding initial values
    WSMInputFunctionsAutomaticoverriding input values
    WSMParameterValuesAutomaticoverriding parameter values
    WSMProgressMonitorAutomaticcontrol display of progress
  • The option setting Automatic normally means that the setting is taken from "mmodel" or its experiment setting.
  • Setting WSMParameterValues or WSMInitialValues to {pi->{c1,c2,…},…} runs simulations in parallel, with pi taking values cj.
  • WSMInitialValues corresponds to the start property in the Modelica model.
  • WSMInputFunctions->{"var1"->fun1,…} uses funi[t] as the input value for vari at time t.
  • The CVODES solver used can be controlled with Method->{"opt1"->val1}.
  • Possible suboptions for the CVODES method include:
  • "InterpolationPoints"Automaticnumber of interpolation points
    "Tolerance"106tolerance for adaptive step size

Examples

open allclose all

Basic Examples  (4)

Load Wolfram SystemModeler Link:

Study sensitivity of a parameter over the time interval in model experiment settings:

Show the sensitivity of a signal to relative changes in a parameter:

Plot bounds for y and z when varying a by 10%:

Use the diagram representation of a model as input:

Copy and paste the output above:

Scope  (10)

Simulation Time  (3)

Simulate with settings from the model:

Simulate from time 0 to 5:

Simulate for an explicit time interval:

Sensitivity Results  (6)

Study the sensitivity of one parameter:

Simulate with sensitivity to parameter a:

Get the sensitivity names:

Get the sensitivity y has to changes in a:

Study the sensitivities from one parameter:

Plot one of the sensitivities:

Show the sensitivity of a signal to a parameter:

Simulate with sensitivity to a:

Get the sensitivity names:

Get the sensitivity y has to changes in a, as well as the nominal trajectory for y:

Plot y with original parameter a, and with parameter a increased by 0.05:

Show the sensitivity of a signal to relative changes in a parameter:

Get the sensitivity names:

Get the sensitivity y and z have to changes in a, as well as nominal trajectories and value:

Plot bounds for y and z when varying a by 10% of the sensitivity:

Show the sensitivity of a signal to absolute changes in a parameter:

Simulate with sensitivity to a:

Get the sensitivity y has to changes in a, as well as the trajectory for y:

Compute the change in y when parameter a changes with absolute value 0.1:

Plot the variation of y when parameter a varies by ±0.1:

Result Storage  (1)

Store only selected variables:

Only the given variables and parameters are saved:

Generalizations & Extensions  (1)

Debug messages are collected in the message group "WSMLinkDebug":

Turn on debug messages for initialization:

Turn off all debug messages for WSMLink:

Options  (5)

InterpolationOrder  (1)

Simulate with interpolation orders 1 and 3, and 3 interpolation points:

Show the sensitivity variable:

WSMInitialValues  (1)

Change the initial values of a simulation:

Compare the changes in a plot:

WSMInputFunctions  (1)

Give an input function for a variable and study the sensitivity of the output:

Simulate the model that integrates the input after applying a gain:

Plot the sensitivity of the output to the gain parameter:

WSMParameterValues  (1)

Change the parameter values of a simulation:

Compare the two in a plot:

WSMProgressMonitor  (1)

Turn off the progress dialog with WSMProgressMonitor:

Applications  (5)

Study the sensitivity of a model:

Get the value of the parameter:

Find the peak deviation when varying the parameter:

Show a 5% sensitivity bound and the peak deviation time:

Find out which variable is most sensitive to a parameter:

Simulate with sensitivities to a frequency parameter:

A 10% sensitivity bound shows that "integrator3.y" is most sensitive to the parameter:

Simulate a rolling wheel:

Select the position of the wheel and its sensitivities to different parameters:

Show the path of the wheel with 4% variation of the wheel radius and mass, respectively:

Calibrate parameters in a model by comparing to measurement data:

Set up caching for simulation:

Use WSMSimulateSensitivity to get gradients:

Fit parameters to the measurement data:

Not using gradients takes longer:

Simulate with the fitted parameters:

Show the test data and the calibrated model together:

Plot a solution with its sensitivity bounds:

Get the nominal value of the parameter:

Show a 5% sensitivity bound:

Simulate with a maximal variation of 5%:

Get the trajectories:

Show that the trajectories are mostly contained in the approximated sensitivity bounds:

Properties & Relations  (4)

Compare a sensitivity simulation with the sensitivity of the corresponding differential equation:

Plot bounds for a relative parameter change:

Get the sensitivity y has to changes in a, as well as y and the value for a:

Plot bounds for y when varying a by 10% of the sensitivity:

Use WSMPlot instead:

Sensitivities are valid for small changes in the parameter:

Get sensitivities to a parameter:

Simulate with variation of the parameter:

Comparing in a plot, a 10% variation gives trajectories outside computed bounds:

Use WSMParametricSimulate for a function that can be evaluated for different values:

Compute solutions for different values of the frequency parameter:

Plot the solutions over time:

Neat Examples  (1)

Show sensitivity bounds for the and axes in the Rabinovich–Fabrikant equations:

Show the sensitivity bounds in 3D: