|
3.11.4 CompressMatrixEquation

Command structure of CompressMatrixEquation.
Computing a transfer function from a linear system of circuit equations 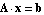 requires solving the matrix equation for one single variable requires solving the matrix equation for one single variable  . The values of all other variables . The values of all other variables  , , 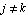 , are of no interest in this context. Systems of circuit equations usually contain a significant amount of information which is only needed to determine the irrelevant variables, and the proportion of such information increases during the approximation process as equations are algebraically decoupled by removing negligible terms. , are of no interest in this context. Systems of circuit equations usually contain a significant amount of information which is only needed to determine the irrelevant variables, and the proportion of such information increases during the approximation process as equations are algebraically decoupled by removing negligible terms.
To reduce the computational effort needed for solving an approximated matrix, all unnecessary information should be discarded from the equations prior to calling Solve, using the function CompressMatrixEquation. This function performs a recursive search on a matrix equation to find and delete all rows and columns which are not needed to compute the variable of interest. Note that compressing a matrix equation is a mathematically exact operation which does not change the value of the output variable.
CompressMatrixEquation has the following option:

Option for CompressMatrixEquation.
See also: CompressNonlinearEquations, ApproximateMatrixEquation.
Examples
Load Analog Insydes.
In[1]:= <<AnalogInsydes`
Define an AC model for BJTs.
In[2]:= Circuit[
Model[
Name -> BJT,
Selector -> AC,
Scope -> Global,
Ports -> {B, C, E},
Parameters -> {Rbe, Cbc, Cbe, beta, Ro,
RBE, CBC, CBE, BETA, RO},
Definition -> Netlist[
{CBE, {B, E}, Symbolic -> Cbe, Value -> CBE},
{RBE, {X, E}, Symbolic -> Rbe, Value -> RBE},
{CBC, {B, C}, Symbolic -> Cbc, Value -> CBC},
{CC, {B, X, C, E},
Symbolic -> beta, Value -> BETA},
{RO, {C, E}, Symbolic -> Ro, Value -> RO}
]
]
] // ExpandSubcircuits;
This netlist describes a common-emitter amplifier.
In[3]:= ceamplifier =
Circuit[
Netlist[
{V1, {1, 0}, 1},
{V0, {6, 0}, 0},
{C1, {1, 2}, Symbolic -> C1, Value -> 1.0*^-7},
{R1, {2, 6}, Symbolic -> R1, Value -> 1.0*^5},
{R2, {2, 0}, Symbolic -> R2, Value -> 47000.},
{RC, {6, 3}, Symbolic -> RC, Value -> 2200.},
{RE, {4, 0}, Symbolic -> RE, Value -> 1000.},
{C2, {3, 5}, Symbolic -> C2, Value -> 1.0*^-6},
{RL, {5, 0}, Symbolic -> RL, Value -> 47000.},
{Q1, {2 -> B, 3 -> C, 4 -> E},
Model -> BJT, Selector -> AC,
CBE -> 30.*^-12, CBC -> 5.*^-12, RBE -> 1000.,
RO -> 10000., BETA -> 200.}
]
]
Out[3]= 
Set up a system of symbolic AC equations.
In[4]:= eqs = CircuitEquations[ceamplifier,
ElementValues -> Symbolic]
Out[4]= 
Approximate the system of circuit equations.
In[5]:= sbg = ApproximateMatrixEquation[eqs, V$5,
{s -> 2. Pi I 10^4, MaxError -> 0.1}]
Out[5]= 
Inspect the list of unknowns in the matrix equation.
In[6]:= GetVariables[sbg]
Out[6]= 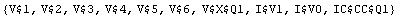
Solve the equations for V$5.
In[7]:= Solve[sbg, V$5]
Out[7]= 
Discard rows and columns which are not needed to compute V$5.
In[8]:= cmat = CompressMatrixEquation[sbg, V$5]
Out[8]= 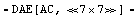
Inspect the list of remaining unknowns.
In[9]:= GetVariables[cmat]
Out[9]= 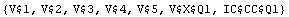
Note that matrix compression does not change the solution of the equations.
Solve the compressed equations for V$5.
In[10]:= Solve[cmat, V$5]
Out[10]= 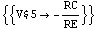
|