|
3.8.1 GeneralizedEigensystem

Command structure of GeneralizedEigensystem.
GeneralizedEigensytem computes the eigenvalues and the corresponding left and right eigenvectors of a matrix pencil 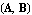 by the QZ algorithm. The function returns a list of lists of the form {{lambda, v, u, iter}, by the QZ algorithm. The function returns a list of lists of the form {{lambda, v, u, iter},  }, where lambda denotes a finite eigenvalue of }, where lambda denotes a finite eigenvalue of 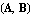 , v and u the corresponding left and right eigenvectors, and iter the number of iterations the QZ algorithm needed to compute lambda. , v and u the corresponding left and right eigenvectors, and iter the number of iterations the QZ algorithm needed to compute lambda.
Note that this function is accessible only if the global Analog Insydes option UseExternals is set to True and if a native version of the external MathLink module QZ.exe is available for your machine (see Section 3.13.4).
GeneralizedEigensystem has the following option:

Option for GeneralizedEigensystem.
Unless you specify Normalize -> False, the eigenvectors are scaled such that 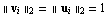 . .
See also: GeneralizedEigenvalues, UseExternals.
Examples
Load Analog Insydes.
In[1]:= <<AnalogInsydes`
Define two square real-valued matrices.
In[2]:= A = {{1, 2}, {-3, 1}};
B = {{1, -1}, {0, 0}};
Compute the eigenvalues and eigenvectors of  . .
In[3]:= eigsys = GeneralizedEigensystem[A, B]
Out[4]= 
Get the eigenvalue and corresponding eigenvectors.
In[4]:= {lambda, v, u, iter} = First[eigsys];
To show that lambda, v, and u are indeed solutions of the GEP within machine precision, we compute the 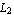 norms of the residual vectors norms of the residual vectors 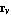 and and  : :
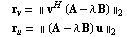
Compute the residual norms.
In[5]:= {L2Norm[Conjugate[v].(A - lambda*B)],
L2Norm[(A - lambda*B).u]}
Out[6]= 
|