|
3.8.2 GeneralizedEigenvalues

Command structure of GeneralizedEigenvalues.
GeneralizedEigenvalues computes the eigenvalues of a matrix pencil 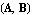 by the QZ algorithm. The function returns a list of the finite by the QZ algorithm. The function returns a list of the finite  that satisfy the GEP defined by that satisfy the GEP defined by 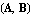 . .
Note that this function is accessible only if the global Analog Insydes option UseExternals is set to True and if a native version of the external MathLink module QZ.exe is available for your machine (see Section 3.13.4).
See also: GeneralizedEigensystem, UseExternals.
Examples
Load Analog Insydes.
In[1]:= <<AnalogInsydes`
Define two square real-valued matrices.
In[2]:= A = {{1, 2}, {-3, 1}};
B = {{1, 4}, { 2, 1}};
Compute the eigenvalues of  . .
In[3]:= GeneralizedEigenvalues[A, B]
Out[4]= 
GeneralizedEigenvalues also works if some or all of the eigenvalues are complex and in the case where 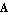 or or 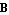 are singular. are singular.
Define two further  matrices. matrices.
In[4]:= B2 = {{1, -5}, {2, 1}};
B3 = {{1, -1}, {0, 0}};
Compute the eigenvalues of 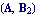 . .
In[5]:= GeneralizedEigenvalues[A, B2]
Out[7]= 
Compute the eigenvalues of  . .
In[6]:= GeneralizedEigenvalues[A, B3]
Out[8]= 
|