|
3.8.3 PolesAndZerosByQZ

Command structure of PolesAndZerosByQZ.
To calculate the poles and zeros of a linear circuit, the coefficient matrix of the corresponding system of circuit equations must be decomposed into a matrix pencil 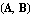 . PolesAndZerosByQZ performs this decomposition and calls GeneralizedEigenvalues to compute the poles and zeros numerically. The argument dae must be an AC DAEObject written in matrix form (see CircuitEquations in Section 3.5.1). . PolesAndZerosByQZ performs this decomposition and calls GeneralizedEigenvalues to compute the poles and zeros numerically. The argument dae must be an AC DAEObject written in matrix form (see CircuitEquations in Section 3.5.1).
PolesAndZerosByQZ returns a list of rules of the form:
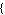 Poles -> Poles -> 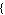 poles poles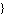 , Zeros -> , Zeros ->  zeros zeros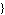 
The return value can directly be used as input for RootLocusPlot for visualizing the pole/zero distribution.
 Note that this function is accessible only if the global Analog Insydes option UseExternals is set to True and if a native version of the external MathLink module QZ.exe is available for your machine (see Section 3.13.4).
See also: PolesByQZ, ZerosByQZ, RootLocusPlot, UseExternals.
Examples
Load Analog Insydes.
In[1]:= <<AnalogInsydes`
Read in a PSpice netlist and small-signal data.
In[2]:= buffer = ReadNetlist[
"AnalogInsydes/DemoFiles/Buffer.cir",
"AnalogInsydes/DemoFiles/Buffer.out",
Simulator -> "PSpice"]
Out[2]= 
Set up a system of AC equations.
In[3]:= mnabuffer = CircuitEquations[buffer, AnalysisMode -> AC]
Out[3]= 
Calculate both poles and zeros with respect to the output voltage V$99 of the circuit.
In[4]:= pz = PolesAndZerosByQZ[mnabuffer, V$99]
Out[4]= 
Show the pole/zero distribution.
In[5]:= RootLocusPlot[pz, LinearRegionLimit -> Infinity,
PlotRange -> 5.0*^6]
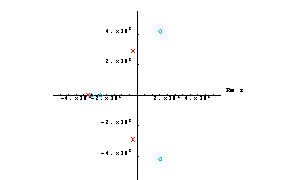
Out[5]= 
|