2.7.3 Flow of Transient Circuit Analysis

A Summary of the Transient Analysis Procedure

In this subsection, we summarize the steps which are necessary to perform a transient analysis of a dynamic circuit with Analog Insydes.

1) Write a netlist of the circuit to be simulated, specifying numerical values for all circuit elements or use ReadNetlist for automatically importing netlists from external simulator files.

circuit =

Circuit[

Netlist[],

Model[],



]

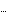
2) Set up a system of time-domain circuit equations using CircuitEquations with the option setting AnalysisMode -> Transient. For numerical circuit simulation you should use modified nodal analysis, which is the default formulation. Modified nodal equations are smaller in size and therefore require less simulation time.

mnaequations =

CircuitEquations[circuit, AnalysisMode -> Transient]

3) Apply the command NDAESolve to the circuit equations to calculate the transient solution in the time interval , where is usually zero.

transient = NDAESolve[mnaequations, , , ]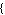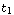

4) Use TransientPlot for transient waveform display. Select the variables to be plotted by means of the list vars and specify the display time interval . The latter need not be the same as the simulation time interval . You can use any other values for and to zoom in onto a particular section of a trace as long as the condition holds.

TransientPlot[transient, vars, , , ]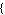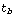

NDAESolve Program Flow

Now, let's take a closer look at the strategy NDAESolve employs to integrate a system of differential and algebraic equations. The main idea behind the algorithm is to transform the problem of solving a nonlinear system of differential and algebraic equations into a sequence of linear and purely algebraic problems which can be solved rather easily. The transformation is carried out in two stages. In the first step, the differential equations are discretized by replacing all time derivatives with a finite difference approximation. The differential equations are thus evaluated and solved at discrete time steps only. The finite difference approximation scheme used by NDAESolve is an implicit integration method known as the trapezoidal rule. In a second step the resulting nonlinear algebraic system of equations is then solved for the voltages and currents using the multi-dimensional Newton-Raphson method.

Circuit equations are usually stiff, which means that their solutions involve both very rapid and very slow transients. To avoid loss of accuracy and convergence problems during rapid transients as well as excessive computation time requirements for slow transients the step size is chosen adaptively at each time step according to the curvature of the waveform. Whenever a waveform changes quickly the step size is cut back whereas it is increased during periods of latency. The behavior of the step size control algorithm depends on the values of five parameters which will be discussed in the following section. The associated NDAESolve options by which the default parameter settings can be changed are StartingStepSize, MaxStepSize, MinStepSize, StepSizeFactor, and MaxDelta.

Figure 7.3 shows a flow graph of the algorithm implemented in NDAESolve.

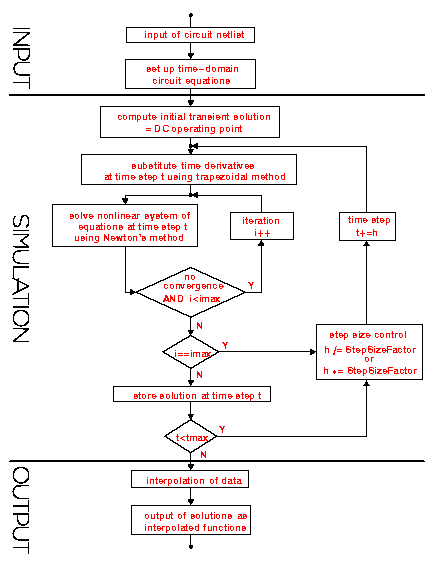
Figure 7.3: NDAESolve program flow