6.1.7 Fourier CamsAnother method of modeling arbitrary cam profiles is by approximating the cam profile with a Fourier series of sine and cosine functions. This method guarantees a continuously differentiable cam profile and also may evaluate more quickly than a SplineFunction object, provided only a relatively small number of terms are retained. One disadvantage of a Fourier series based cam profile is that it does not pass exactly through the data points used to generate it.
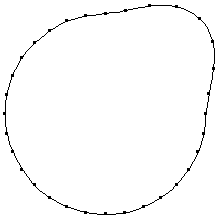
The following example uses a series of points in Cartesian coordinates that are to lie on the surface of a closed cam profile. The profile has a protruding lobe for 1/4 of a turn and is approximately circular with a radius of 3.0 for the next 3/4 of a turn. The built-in Mathematica Fourier function is used to generate the Fourier series. Here is the data to be transformed. Fourier is used to transform the data. Note that the zero-frequency term in each series must be divided by two to map correctly back into the time domain with Sin and Cos functions. Here are the first 10 terms of the approximate periodic function. Here is a plot of the Fourier profile along with the data points.
Out[57]= |  |
|