13.2.1 Inconsistent Constraints

The most basic error in kinematic modeling is to simply define a set of constraints that is not consistent with the mechanism that is being modeled. If a model to which no solution exists is defined, Mech must fail to converge.
For example, consider a rotating crank with a single link between an eccentric point on the crank and a point on the ground. If the link is insufficiently long, it will not reach from the crank to the ground, regardless of the orientation of the crank. In this case, the link is only 1.75 units long, while the minimum possible distance between its two attachment points is 2 units. No assembled configuration of the mechanism exists, so the Newton-Rhapson solution block fails.

This loads the Modeler2D package.

In[1]:=

Here is a simple crank-with-link mechanism.

In[2]:=

SolveMech attempts to find a solution, but it cannot.

In[4]:=

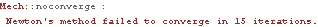
Out[5]=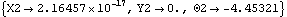

The diagnosis of this type of problem can be quite difficult. No specific tool to help isolate such a problem is provided by Mech because Mathematica can only know what is said, not what is meant.
The first thing to try is usually to make a quick sketch of the mechanism, and make sure that its assembly is feasible. If it is clear that the problem is a modeling error, not a conceptual one, then an examination of the constraint expressions can yield some insight.

Here are the current values of constraints 1 and 2.

In[6]:=

Out[6]=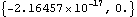

Out[7]=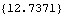

Since the expressions in constraint 1 are equal to zero at the current values of the initial guesses, they are satisfied and are probably not the cause of the problem. Constraint 2, the RelativeDistance1 constraint, is not equal to zero, therefore it is the constraint that SolveMech was unable to satisfy.
While this method may prove to be helpful in isolating a problem, there is no guarantee that a constraint that is not satisfied is actually the one that is in error. For example, it is possible that the length of the link in the example is correct and is what the designer intended, and what really needs correction is the location of the center of the crank.
Another tool that can prove helpful is StepMech. This function causes the iterative solver to take a single Newton-Rhapson step toward the solution and return the result, regardless of any convergence criteria. This allows the solution to be inspected at each step, so that if it starts to diverge, the user can see "which way it goes".

A debugging utility.

StepMech is equivalent to SolveMech with MaxIterations set to 1, and an infinitely accurate convergence criteria.