13.2 Failure to ConvergeThis section deals with mechanism modeling errors that prevent a Mech model from converging to a solution or cause it to converge to an incorrect solution. 13.2.1 Inconsistent ConstraintsThe most basic error in kinematic modeling is to simply define a set of constraints that is not consistent with the mechanism that is being modeled. If a model to which no solution exists is defined, Mech must fail to converge.
For example, consider a rotating crank with a single link between an eccentric point on the crank and a point on the ground. If the link is insufficiently long, it will not reach from the crank to the ground, regardless of the orientation of the crank. In this case, the link is only 1.75 units long, while the minimum possible distance between its two attachment points is 2 units. No assembled configuration of the mechanism exists, so the Newton-Rhapson solution block fails. This loads the Modeler2D package. Here is a simple crank-with-link mechanism. SolveMech attempts to find a solution, but it cannot.
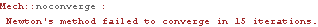
Out[5]= | 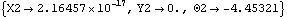 |
The diagnosis of this type of problem can be quite difficult. No specific tool to help isolate such a problem is provided by Mech because Mathematica can only know what is said, not what is meant.
The first thing to try is usually to make a quick sketch of the mechanism, and make sure that its assembly is feasible. If it is clear that the problem is a modeling error, not a conceptual one, then an examination of the constraint expressions can yield some insight. Here are the current values of constraints 1 and 2.
Out[6]= | 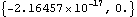 |
Out[7]= | 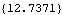 |
Since the expressions in constraint 1 are equal to zero at the current values of the initial guesses, they are satisfied and are probably not the cause of the problem. Constraint 2, the RelativeDistance1 constraint, is not equal to zero, therefore it is the constraint that SolveMech was unable to satisfy.
While this method may prove to be helpful in isolating a problem, there is no guarantee that a constraint that is not satisfied is actually the one that is in error. For example, it is possible that the length of the link in the example is correct and is what the designer intended, and what really needs correction is the location of the center of the crank.
Another tool that can prove helpful is StepMech. This function causes the iterative solver to take a single Newton-Rhapson step toward the solution and return the result, regardless of any convergence criteria. This allows the solution to be inspected at each step, so that if it starts to diverge, the user can see "which way it goes".

A debugging utility. StepMech is equivalent to SolveMech with MaxIterations set to 1, and an infinitely accurate convergence criteria. 13.2.2 BifurcationAnother common modeling problem is bifurcation, a condition where more than one solution to the system of constraint equations exists, representing multiple possible assembled configurations. When the previously defined crank-with-link model is modified so that it can converge, it is able to converge to either of two solutions depending on the values of the initial guesses. Here is one possible configuration of the crank-with-link model with a reasonable value of len.
Out[10]= | 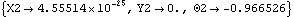 |
And here is the other possible configuration of the crank-with-link model.
Out[12]= | 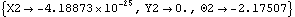 |
Once a model is apparently functioning properly, the value of a graphic image of the model cannot be overemphasized. A rudimentary graphic image can immediately show errors that may have gone unnoticed, such as the fact that a model has converged on the wrong side of a bifurcation, or simply that the model has been defined incorrectly. Errors that are difficult to detect from the numbers alone are often easily seen in the graphic. Here is a simple graphic of the crank-with-link model at both positions.
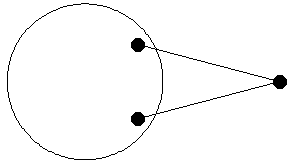
Out[13]= | 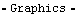 |
13.2.3 RedundancyA mechanism model with a redundant constraint set can be thought of as having more than one constraint controlling the same degree of freedom. Since SetConstraints only allows models to be defined if they have equal numbers of constraints and degrees of freedom, the presence of one redundant constraint implies the presence of one unconstrained degree of freedom. CheckSystem may be used to detect such errors. Here is a model with a redundant constraint set.

The constraint position numbers given in the error message generated by CheckSystem refer to the position of the offending constraints in the current constraint list. For example, the current constraint vector has three expressions, the first two from Translate2 and the last from Orthogonal1. The positions {{1, 1}, {2, 1}} given by the error message refers to the first expression in constraint 1, the Translate2, and the first and only expression in constraint 2, the Orthogonal1.
CheckSystem is usually, but not always, able to detect redundancies in a constraint set. Because of the Euler generalized parameters used in the 3D constraint formulation, it is possible for CheckSystem to be unable to detect a redundancy if the current initial guesses for the Euler parameters do not constitute a valid set.
Specifically, a valid set of four Euler parameters representing an arbitrary angular orientation must satisfy the following relation.
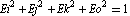
If the Euler parameters in the current initial guesses do not satisfy this relationship, it is possible for CheckSystem to be unable to detect a redundant constraint set.
Another weakness in the redundancy checking used by Mech is that numerical inaccuracies may cause CheckSystem to report that more constraint expressions are participating in a redundancy than really are. This is only a problem in relatively large systems where numerical errors are more pronounced.
|