|
13. Debugging Models OverviewThis chapter is intended to help MechanicalSystems users to diagnose and repair common errors in mechanism models. There is a penalty to be paid for the tremendous flexibility available within any symbolic Mathematica model, that is, an equally tremendous number of ways that a model can fail. This chapter can only scratch the surface of the full breadth of possible modeling errors that can occur in a Mech model, but the basic debugging methods presented should be applicable to all models that are so afflicted. 13.1 Model Building ErrorsThis section deals with model building errors that prevent Mech from building the constraint or load expressions or prevent the completed model from running. 13.1.1 Bad ArgumentsMech functions are written with as much type checking as is possible without restricting the user from incorporating arbitrary mathematical expressions into a model. Unfortunately, this caveat means that there can be essentially no type checking on any symbolic argument that is intended to evaluate to a number.
Many arguments to Mech functions are type checked, such as point and vector arguments, but since point objects and vector objects may also contain symbolic expressions buried in their local coordinates, these items cannot be rigorously type checked until runtime. The following examples show where Mech's type checking catches bad arguments and where others slip through. This loads the Modeler2D package. A Mech body, constraint, or load function is returned unevaluated if it is called with invalid arguments. For example, the Translate2 constraint expects a pair of axis objects that have the head Axis or Line. If Translate2 recognizes that these arguments are incorrect, the entire constraint function is returned unevaluated. Here is a misspelled axis object.

Out[2]= | 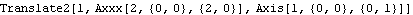 |
If a constraint function is passed the correct argument types, but the contents of these arguments are invalid, a constraint object is returned with some assumptions made about what to do with the invalid arguments. In the following example, the 3D point specification is not recognized by Modeler2D, so Point[2, {1,0,0}] is replaced with Point[2, {0,0}]. This is certainly not what the user intended, but it causes a valid constraint object to be returned. Here is a constraint with a 3D local coordinate that should be 2D.

Out[3]= | 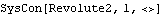 |
The types of errors shown above are diagnosed fairly easily. More elusive problems result when a bad value is given for arguments of type expr. When a Mech usage statement specifies that an argument of type expr is required, it means any expression that will evaluate to a number at runtime may be used. Mathematica has no way of telling in advance whether or not an expression will evaluate to a number, so these arguments cannot be type checked at all. Here is a constraint with an unchecked expression argument.
Out[4]= | 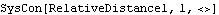 |
The last argument to the RelativeDistance1 constraint (2 a) is supposed to evaluate to a number. If, at runtime, the symbol a evaluates to a number, then the constraint is valid. If the symbol a has no definition, or it evaluates to a List or other function at runtime, then Mech will fail. Mathematica has no way of knowing what the symbol a will do at runtime, so it cannot be type checked.
Note that the first argument of a SysCon object is a list of the constraint expressions contained in the object. Here are the constraint expressions contained in cs.
Out[5]= | 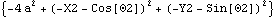 |
13.1.2 Constraint InspectionWhen an expression in a Mech model is supposed to evaluate to a number but it does not, it can often be caught by the CheckSystem function. CheckSystem evaluates the constraint expressions in the current model, subject to the current initial guesses and parameters, and reports any nonnumeric expressions found. Consider the following simple model of a reciprocating slider. If CheckSystem is run before the symbols amp and freq are defined, they are identified. Here is a reciprocating slider model.

If the symbols amp and freq are defined at runtime, but not defined in such a way that the expression amp Sin[freq T] evaluates to a number, CheckSystem cannot determine exactly what is wrong. Here is a bogus definition for the symbol freq.

The constraint inspection function. Constraints is a Mech function that is used to return all or part of the vector of constraint expressions in the current model. Often, direct inspection of the constraints immediately gives a clue as to the cause of an error. Usually, the constraints are inspected subject to the values of the current guesses and parameters, which shows exactly what CheckSystem saw to be an error. Here is the entire current constraint vector.
Out[12]= | 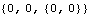 |
In all cases, input such as this should return a vector of numbers. In this case, the third constraint expression evaluates to a list of numbers, instead of a single number. Obviously this is due to the bogus definition of freq = {2, 4} in the example. We can repair the bogus definition and try again.
Out[15]= | 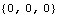 |
Now the constraints evaluate to a list of numbers, as is required. The fact that each of the constraint expressions evaluates to zero simply means that all of the constraints are perfectly satisfied at the current values of the initial guesses, which is not usually the case. 13.1.3 Load InspectionMech load expressions may be rendered invalid by the presence of nonnumeric expressions in the same way as constraint expressions. CheckSystem evaluates the current load expressions, if any exist, subject to the current values of the initial guesses, parameters, and Lagrange multipliers, and reports any nonnumeric expressions found. To demonstrate, a simple load is added to the reciprocating slider model defined in Section 13.1.2. A force applied to body 2.
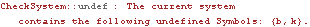
If the symbols k and b are defined at runtime, but not defined in such a way that the expression Exp[k t + b] evaluates to a number, CheckSystem will not be able to determine exactly what is wrong. For example, CheckSystem is limited to recognizing raw symbols only. CheckSystem does not recognize a user-defined variable of the form c[n].

The load inspection function. Loads is a Mech function that is used to return all or part of the vector of load expressions that are applied to the current model. Usually, the loads are inspected subject to the values of the current guesses, parameters, and Lagrange multipliers, which shows exactly what CheckSystem saw to be an error. Here is the current vector of applied loads.
Out[22]= | 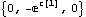 |
In all cases, the input shown should return a list of numbers. In this case, the second load expression, the Y component of the force applied to body 2, evaluates to a symbolic expression instead of a single number. Obviously this is due to the definition of b = c[1] given.
However, c[2] does not appear in the applied loads. This is because c[2] (k) is multiplied by time T. The current initial guess for T is T -> 0, so c[2] is canceled entirely. Thus, CheckSystem does not even recognize the presence of c[2] until the initial guesses are perturbed. We can repair one of the bogus definitions, but the other still remains.
Out[24]= | 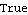 |
CheckSystem thinks that all is well, which is definitely not the case. This is an often frustrating flaw in CheckSystem, but it cannot tell what is and is not a number until it evaluates it, and zero times anything is a number. If the value of time is perturbed, CheckSystem sees that the loads are not purely numeric. If we change the current value of time with SetGuess, CheckSystem recognizes an error.

Now we repair the other bogus definition.
Out[29]= | 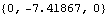 |
Now the loads evaluate to a nested list of numbers, as is required. 13.2 Failure to ConvergeThis section deals with mechanism modeling errors that prevent a Mech model from converging to a solution or cause it to converge to an incorrect solution. 13.2.1 Inconsistent ConstraintsThe most basic error in kinematic modeling is to simply define a set of constraints that is not consistent with the mechanism that is being modeled. If a model to which no solution exists is defined, Mech must fail to converge.
For example, consider a rotating crank with a single link between an eccentric point on the crank and a point on the ground. If the link is insufficiently long, it will not reach from the crank to the ground, regardless of the orientation of the crank. In this case, the link is only 1.75 units long, while the minimum possible distance between its two attachment points is 2 units. No assembled configuration of the mechanism exists, so the Newton-Rhapson solution block fails. This loads the Modeler2D package. Here is a simple crank-with-link mechanism. SolveMech attempts to find a solution, but it cannot.
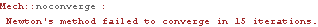
Out[5]= | 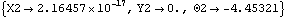 |
The diagnosis of this type of problem can be quite difficult. No specific tool to help isolate such a problem is provided by Mech because Mathematica can only know what is said, not what is meant.
The first thing to try is usually to make a quick sketch of the mechanism, and make sure that its assembly is feasible. If it is clear that the problem is a modeling error, not a conceptual one, then an examination of the constraint expressions can yield some insight. Here are the current values of constraints 1 and 2.
Out[6]= | 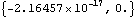 |
Out[7]= | 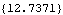 |
Since the expressions in constraint 1 are equal to zero at the current values of the initial guesses, they are satisfied and are probably not the cause of the problem. Constraint 2, the RelativeDistance1 constraint, is not equal to zero, therefore it is the constraint that SolveMech was unable to satisfy.
While this method may prove to be helpful in isolating a problem, there is no guarantee that a constraint that is not satisfied is actually the one that is in error. For example, it is possible that the length of the link in the example is correct and is what the designer intended, and what really needs correction is the location of the center of the crank.
Another tool that can prove helpful is StepMech. This function causes the iterative solver to take a single Newton-Rhapson step toward the solution and return the result, regardless of any convergence criteria. This allows the solution to be inspected at each step, so that if it starts to diverge, the user can see "which way it goes".

A debugging utility. StepMech is equivalent to SolveMech with MaxIterations set to 1, and an infinitely accurate convergence criteria. 13.2.2 BifurcationAnother common modeling problem is bifurcation, a condition where more than one solution to the system of constraint equations exists, representing multiple possible assembled configurations. When the previously defined crank-with-link model is modified so that it can converge, it is able to converge to either of two solutions depending on the values of the initial guesses. Here is one possible configuration of the crank-with-link model with a reasonable value of len.
Out[10]= | 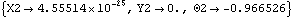 |
And here is the other possible configuration of the crank-with-link model.
Out[12]= | 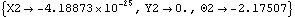 |
Once a model is apparently functioning properly, the value of a graphic image of the model cannot be overemphasized. A rudimentary graphic image can immediately show errors that may have gone unnoticed, such as the fact that a model has converged on the wrong side of a bifurcation, or simply that the model has been defined incorrectly. Errors that are difficult to detect from the numbers alone are often easily seen in the graphic. Here is a simple graphic of the crank-with-link model at both positions.
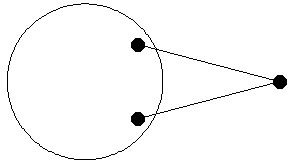
Out[13]= |  |
13.2.3 RedundancyA mechanism model with a redundant constraint set can be thought of as having more than one constraint controlling the same degree of freedom. Since SetConstraints only allows models to be defined if they have equal numbers of constraints and degrees of freedom, the presence of one redundant constraint implies the presence of one unconstrained degree of freedom. CheckSystem may be used to detect such errors. Here is a model with a redundant constraint set.

The constraint position numbers given in the error message generated by CheckSystem refer to the position of the offending constraints in the current constraint list. For example, the current constraint vector has three expressions, the first two from Translate2 and the last from Orthogonal1. The positions {{1, 1}, {2, 1}} given by the error message refers to the first expression in constraint 1, the Translate2, and the first and only expression in constraint 2, the Orthogonal1.
CheckSystem is usually, but not always, able to detect redundancies in a constraint set. Because of the Euler generalized parameters used in the 3D constraint formulation, it is possible for CheckSystem to be unable to detect a redundancy if the current initial guesses for the Euler parameters do not constitute a valid set.
Specifically, a valid set of four Euler parameters representing an arbitrary angular orientation must satisfy the following relation.
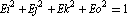
If the Euler parameters in the current initial guesses do not satisfy this relationship, it is possible for CheckSystem to be unable to detect a redundant constraint set.
Another weakness in the redundancy checking used by Mech is that numerical inaccuracies may cause CheckSystem to report that more constraint expressions are participating in a redundancy than really are. This is only a problem in relatively large systems where numerical errors are more pronounced. 13.3 Mathematical AnomaliesIn this section artifacts of the mathematical methods used by Mech are discussed. 13.3.1 Zero Unit VectorsIf the concept of a zero-length unit vector seems a little strange, rest assured that Mech also finds it difficult. Unit vectors are used internally by Mech to generate an applied force vector when the magnitude of the force is specified, and the direction of the force is given as a vector based on mechanism geometry. The applied force vector, in this case, is the supplied direction vector divided by its own magnitude, times the specified force magnitude. If the magnitude of the supplied direction vector becomes zero at some point in the mechanism motion, a singularity results.
The most common occurrence of this problem is in the application of frictional forces. If the negation of the velocity vector of a point is used to specify the direction of a force, the velocity of the point may not go to zero at any point in time when a solution is sought. If it does, Mathematica evaluates 0/0 and produces an error message.
While this is to be expected since a zero vector makes no sense as a direction specification, it can be quite difficult to formulate a workaround. Setting the magnitude of the force equal to zero for all points in time at which the direction vector becomes zero may not work, because this still results in 0*0/0, which is no better than 0/0.

Out[1]= | 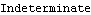 |
The simplest workaround is to use the CutOff option for Force and Moment. A fix for problems with zero-length force vectors. The following example shows the effect that CutOff has on the force vector generated by a Mech Force function. The force is defined with a constant magnitude, but the direction vector of the force is a function of a. Clearly, the force is indeterminate if a goes to zero. Here is a force that fails if a = 0.
Out[3]= | 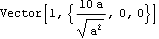 |
Here is the same force using the CutOff option.
Out[4]= | 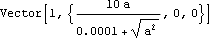 |
The value of CutOff should be extremely small so that it has a negligible effect on the magnitude of the load in the operating range of the variable a. 13.4 Equations of MotionThis section shows how to access the complete system of equations that is generated by a Mech model. 13.4.1 Internal Expression AccessThe following functions are used to access the symbolic expressions that are generated by MechanicalSystems. Functions to provide access to internally stored expressions. Functions that return a model's dependent variables. In all of these functions, the body number bnum can be a single positive integer, a list of integers, All, or Rest. The constraint number cnum can be a single positive integer constraint number, a list of integers, All, Euler, or any of the forms of partial constraint specifications accepted by Constraints.
The complete set of equations that are solved by the Static solution block is given by Transpose[Jacobian[_,_]].Generalized[_]  Loads[_]. The equations of motion that are solved by the Dynamic solution block are the Static equations with Centrifugal[_] + MassMatrix[_].Acceleration[_] added to the left-hand side. Loads[_]. The equations of motion that are solved by the Dynamic solution block are the Static equations with Centrifugal[_] + MassMatrix[_].Acceleration[_] added to the left-hand side. 13.4.2 ExamplesHere is a simple model to provide some values for the dependent variables. The model is run with the Dynamic solution option, and very tight convergence criteria. Here are all the kinematic constraint equations.
Out[6]= | 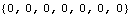 |
Here are the velocity constraints.
Out[7]= | 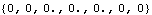 |
Here are the acceleration constraints.
Out[8]= | 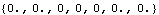 |
Here are the static reaction force equations. They are not satisfied because the model was solved with the Dynamic option.
Out[9]= | 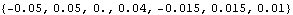 |
Here are the dynamic equations of motion.
Out[10]= | 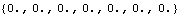 |
|