13.1 Model Building ErrorsThis section deals with model building errors that prevent Mech from building the constraint or load expressions or prevent the completed model from running. 13.1.1 Bad ArgumentsMech functions are written with as much type checking as is possible without restricting the user from incorporating arbitrary mathematical expressions into a model. Unfortunately, this caveat means that there can be essentially no type checking on any symbolic argument that is intended to evaluate to a number.
Many arguments to Mech functions are type checked, such as point and vector arguments, but since point objects and vector objects may also contain symbolic expressions buried in their local coordinates, these items cannot be rigorously type checked until runtime. The following examples show where Mech's type checking catches bad arguments and where others slip through. This loads the Modeler2D package. A Mech body, constraint, or load function is returned unevaluated if it is called with invalid arguments. For example, the Translate2 constraint expects a pair of axis objects that have the head Axis or Line. If Translate2 recognizes that these arguments are incorrect, the entire constraint function is returned unevaluated. Here is a misspelled axis object.

Out[2]= | 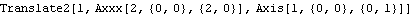 |
If a constraint function is passed the correct argument types, but the contents of these arguments are invalid, a constraint object is returned with some assumptions made about what to do with the invalid arguments. In the following example, the 3D point specification is not recognized by Modeler2D, so Point[2, {1,0,0}] is replaced with Point[2, {0,0}]. This is certainly not what the user intended, but it causes a valid constraint object to be returned. Here is a constraint with a 3D local coordinate that should be 2D.

Out[3]= | 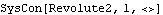 |
The types of errors shown above are diagnosed fairly easily. More elusive problems result when a bad value is given for arguments of type expr. When a Mech usage statement specifies that an argument of type expr is required, it means any expression that will evaluate to a number at runtime may be used. Mathematica has no way of telling in advance whether or not an expression will evaluate to a number, so these arguments cannot be type checked at all. Here is a constraint with an unchecked expression argument.
Out[4]= | 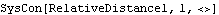 |
The last argument to the RelativeDistance1 constraint (2 a) is supposed to evaluate to a number. If, at runtime, the symbol a evaluates to a number, then the constraint is valid. If the symbol a has no definition, or it evaluates to a List or other function at runtime, then Mech will fail. Mathematica has no way of knowing what the symbol a will do at runtime, so it cannot be type checked.
Note that the first argument of a SysCon object is a list of the constraint expressions contained in the object. Here are the constraint expressions contained in cs.
Out[5]= | 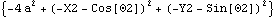 |
13.1.2 Constraint InspectionWhen an expression in a Mech model is supposed to evaluate to a number but it does not, it can often be caught by the CheckSystem function. CheckSystem evaluates the constraint expressions in the current model, subject to the current initial guesses and parameters, and reports any nonnumeric expressions found. Consider the following simple model of a reciprocating slider. If CheckSystem is run before the symbols amp and freq are defined, they are identified. Here is a reciprocating slider model.

If the symbols amp and freq are defined at runtime, but not defined in such a way that the expression amp Sin[freq T] evaluates to a number, CheckSystem cannot determine exactly what is wrong. Here is a bogus definition for the symbol freq.

The constraint inspection function. Constraints is a Mech function that is used to return all or part of the vector of constraint expressions in the current model. Often, direct inspection of the constraints immediately gives a clue as to the cause of an error. Usually, the constraints are inspected subject to the values of the current guesses and parameters, which shows exactly what CheckSystem saw to be an error. Here is the entire current constraint vector.
Out[12]= | 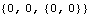 |
In all cases, input such as this should return a vector of numbers. In this case, the third constraint expression evaluates to a list of numbers, instead of a single number. Obviously this is due to the bogus definition of freq = {2, 4} in the example. We can repair the bogus definition and try again.
Out[15]= | 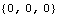 |
Now the constraints evaluate to a list of numbers, as is required. The fact that each of the constraint expressions evaluates to zero simply means that all of the constraints are perfectly satisfied at the current values of the initial guesses, which is not usually the case. 13.1.3 Load InspectionMech load expressions may be rendered invalid by the presence of nonnumeric expressions in the same way as constraint expressions. CheckSystem evaluates the current load expressions, if any exist, subject to the current values of the initial guesses, parameters, and Lagrange multipliers, and reports any nonnumeric expressions found. To demonstrate, a simple load is added to the reciprocating slider model defined in Section 13.1.2. A force applied to body 2.
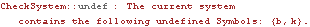
If the symbols k and b are defined at runtime, but not defined in such a way that the expression Exp[k t + b] evaluates to a number, CheckSystem will not be able to determine exactly what is wrong. For example, CheckSystem is limited to recognizing raw symbols only. CheckSystem does not recognize a user-defined variable of the form c[n].

The load inspection function. Loads is a Mech function that is used to return all or part of the vector of load expressions that are applied to the current model. Usually, the loads are inspected subject to the values of the current guesses, parameters, and Lagrange multipliers, which shows exactly what CheckSystem saw to be an error. Here is the current vector of applied loads.
Out[22]= | 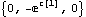 |
In all cases, the input shown should return a list of numbers. In this case, the second load expression, the Y component of the force applied to body 2, evaluates to a symbolic expression instead of a single number. Obviously this is due to the definition of b = c[1] given.
However, c[2] does not appear in the applied loads. This is because c[2] (k) is multiplied by time T. The current initial guess for T is T -> 0, so c[2] is canceled entirely. Thus, CheckSystem does not even recognize the presence of c[2] until the initial guesses are perturbed. We can repair one of the bogus definitions, but the other still remains.
Out[24]= | 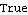 |
CheckSystem thinks that all is well, which is definitely not the case. This is an often frustrating flaw in CheckSystem, but it cannot tell what is and is not a number until it evaluates it, and zero times anything is a number. If the value of time is perturbed, CheckSystem sees that the loads are not purely numeric. If we change the current value of time with SetGuess, CheckSystem recognizes an error.

Now we repair the other bogus definition.
Out[29]= | 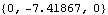 |
Now the loads evaluate to a nested list of numbers, as is required.
|