|
Human Example Mechanism for MechanicalSystemsby Robert Beretta
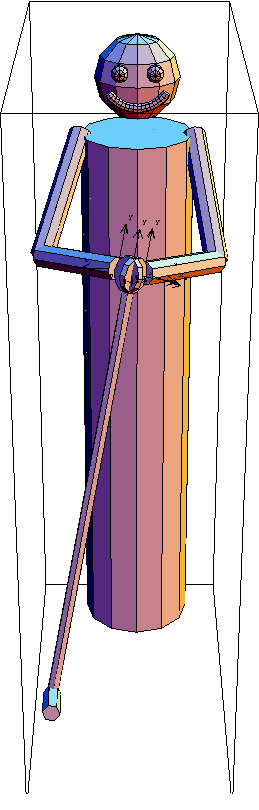  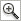
Human GraphicDiscussionThis notebook presents a simple model of the upper body of a human being. The primary intent is to demonstrate modeling techniques that may be useful when modeling 3D systems with many degrees of freedom and some level of static indeterminacy, such as most human beings.
This particular human is using both arms to hold a golf club. The problem here is that one arm is sufficient to fully define the location and orientation of the golf club so some choice must be made as to what constraints to remove from the model to make the model adequately constrained or underconstrained. Two different methods are used to accomplish this. The first method is to drop the excess constraints from one arm to allow the location of the golf club, and hence the second arm, to be determined by the location of the first. The second method is to drop all the constraints that restrict joint mobility from both arms and then apply moments to all the mobile joints that resist any displacement from a neutral position. The underconstrained model then has a statically indeterminate solution that can be found.
The legs of the human are not modeled--the torso simply extends to attach to the ground at the approximate location of the feet. This allows us to easily extract reaction forces at the feet. The reference frame of the human is X->right, Y->forward, and Z->up.
Thanks to Dr. René Ferdinands for inspiring the creation of this model and its inclusion in MechanicalSystems. Kinematic ModelPreparationThe Modeler3D package is loaded into Mathematica with the Needs command. Spelling warnings are disabled because many symbols for the left and right body components have names that differ only slightly. The coordinate system can be set to any of Euler, Angular / Global, or Angular / Local and the model will function equivalently. Performance seems to be slightly superior with Angular / Local. Basic unit vector definitions are useful. Body and Constraint DefinitionsEach body is given a number and a symbolic name. EarthThe earth body lacks any interesting features because it is only used as an anchor for the torso. We could simply omit the earth body from the model and make the torso the ground body, but having the earth body facilitates the easy extraction of the reaction forces at the feet of the human. TorsoTwo constraints attach the torso to the earth at the feet of the human. The origin of the torso is coincident with the origin of the earth. The torso has two attachment points for the upper arms defined in its point list. It has no initial guess specification because the defaults are fine. Upper armsTwo constraints attach each of the upper arms to the torso at the shoulders. The shoulders are modeled as Spherical3 joints with three degrees of rotational freedom that are then constrained with the RotationLock3 constraints. The RotationLock3 constraints will be removed from the model to simulate the human's true freedom of motion. The symbols rt/ltshoulderrot are used to store the relative rotation of the upper arms with respect to the torso. These values are used here to define the orientation offset in the RotationLock3 constraints and they are also used later to define the neutral orientation for the resistance moments that are applied at each joint. The upper arm bodies have initial guesses and attachment points for the lower arms. Lower armsTwo constraints attach each of the lower arms to the upper arms at the elbows. The elbows are modeled as Revolute5 joints (simple hinges) with one degree of rotational freedom that is then constrained with the ProjectedAngle1 constraints. As with the shoulder constraints, earlier, the relative rotations that are used to define the constrained orientation will also be used later to define the neutral orientations for the resistance moments. The lower arm bodies have initial guesses and attachment points for the hands. The initial guesses here are given in Euler parameter form and were experimentally determined during the development of the model. Note that the initial guesses in Euler form do not have to be normalized--this will be done by SetBodies. HandsTwo constraints attach each of the hands to the lower arms at the wrists. The modeling of the wrists is identical to the modeling of the shoulders. The progressive rotations of the right wrist about the X and Y axes will be used later to look at an inverse dynamics solution. The effective angular velocities omx and omy are initially set to zero. The hand bodies have initial guesses and attachment points for the golf club. As with the lower arm bodies, the initial guesses are given in Euler form. Golf clubTwo pairs of constraints attach the golf club to the right or left hands. They cannot be used simultaneously or the model will be overconstrained. The golf club body has an initial guess and a single point to locate the head of the club. It also has nonzero inertia properties so the inverse dynamics will provide some nonzero results. Build the body and constraint definitionsSetBodies accepts the SysBody data objects and adds the information to the MechanicalSystems internal database. SetConstraints accepts the SysCon data objects and adds the information to the MechanicalSystems internal database. Only the constraints for the golf club in the right hand are included at this time. Running the ModelSolve the model at  . Note that the value of T is irrelevant at this time because the angular velocities are set to zero. . Note that the value of T is irrelevant at this time because the angular velocities are set to zero. Here is a graphic for visualization. Here is the golfer with the club in his right hand.
  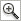
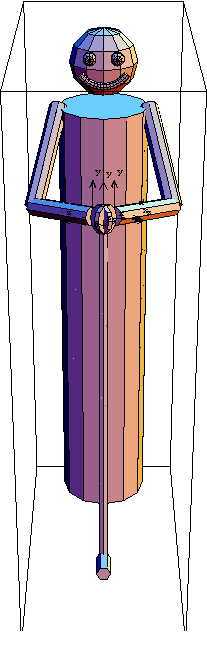
If we build the model with the constraints for the golf club in the left hand, we will see that it is symmetric.

Out of curiosity, let us find out how close the initial guesses are to a valid solution by displaying the model at the initial guess orientation.
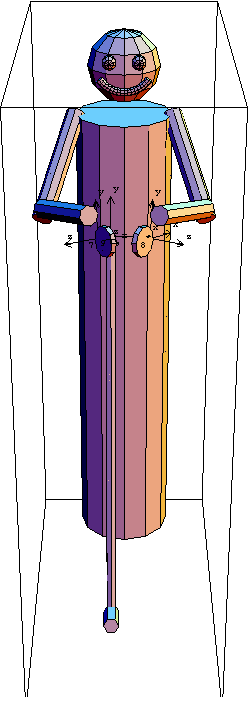  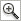
Other Constraint SetsNow we wish to attach the golf club to both hands and drop some constraints from the left arm so that the whole system is still adequately constrained. Attaching the golf club to the left hand will constrain six additional DOFs, but dropping all the constraints that restrict joint mobility from the left arm will unconstrain seven DOFs. A little imagination will allow us to see (since we are all humans?) that if we have one of our hands and our torsos fully constrained then our arms will have one remaining DOF. Our elbows will have the freedom to "flap". One new constraint is added to the model to keep the left elbow from flapping. The left elbow is essentially bound to the torso. This is the full constraint set with the following omissions and additions.
Removed constraint 6. The RotationLock3 that constrains the flexure at the left shoulder.
Removed constraint 10. The ProjectedAngle1 that constrains the flexure at the left elbow.
Removed constraint 14. The RotationLock3 that constrains the flexure at the left wrist.
Added constraint 19. The RelativeDistance1 that keeps the left elbow from flapping. Here is the golfer with the right arm fully constraining the location of the golf club, and the golf club then constraining the location of the left arm.
Static EquilibriumApplied LoadsNow we wish to apply interbody moments at the shoulders, elbows, and wrists that resist any displacement of the joints from a predefined neutral position, and then find a static equilibrium solution with the right arm underconstrained just like the left. The parameter shoulderstiffness will be used to vary the stiffness of the shoulders with respect to the wrists. First, four applied moments resist displacement at the elbows. A careful examination of these moments shows that their specification exactly parallels the two ProjectedAngle1 constraints (cs[9] and cs[10]) that will be dropped from the model. The magnitude of the moments will be zero when the configuration of the elbows is the same as the constrained configuration. Otherwise the applied moment will linearly resist the displacement of each elbow from its constrained configuration.
Note that it would possible to code this as only two moments, not four, by using the form of Moment that takes two body numbers as an argument and applies an equal and opposite moment to each body. However, such a formulation would be less efficient because the direction vector of the moment would always specified in the coordinate system of a different body than the body to which the moment is applied--for one of the two equal and opposite moments. A separate formulation, as is used here, always has the direction vector of the moment specified in the coordinate system of the same body as the body to which the moment is applied. Use Loads[bnum] to interrogate the load vector and see what expressions result from different choices. At each shoulder we have three degrees of rotational freedom and we want the moments at the shoulders to resist any displacement from their constrained configuration. To do this we first develop a rotational displacement vector and use it as the vector of an applied moment, multiplied by a stiffness factor. As we develop the rotational displacement vector, we have three reasonable choices for which coordinate system to express it in--the global coordinate system, the local coordinate system of the torso, or the local coordinate system of the left/right upper arm. Which choice is the best depends on your choice of modeling coordinates--Euler parameters, global angular coordinates, or local angular coordinates.
Because we have chosen to use local angular coordinates to model this human, the best coordinate system choice for applied moments is the local coordinate system of each body. Thus we would develop two independent moment vectors for each arm--one to apply a moment to the arm in the local coordinate system of the arm, and the other to apply an equal and opposite moment to the torso in the local coordinate system of the torso. Such moments would require no coordinate transformation at all before being added to the system load vector.
However, for the sake of simplicity we will develop the shoulder displacement vectors in the global coordinate system and the wrist displacement vectors in their respective local coordinate systems. This choice will cost us the computational burden of a coordinate system transformation in each load applied at the shoulders. Because both moments applied at a single shoulder are in the same coordinate system, we will use the form of Moment that takes two body numbers and applies equal and opposite loads to each--this feature can be used with no penalty only in the global coordinate system.
If we were to use the Euler solution method instead, global coordinates could be used for the loads with no penalty because the forms of the expressions generated by the Euler method are identical in global or local coordinates. The computational efficiency of using two separate Moment objects in the local coordinates of each body would be identical to that of using one Moment object in global coordinates, so the only advantage is that of coding efficiency. If we were to use global angular coordinates for modeling, then global coordinates would be the superior choice for applying moments, for the same reasons that local coordinates are best when modeling in the local coordinate system.
The transformations required to develop the rotational displacement vector are most efficiently done in Euler parameter space, but this is conceptually equivalent to doing them in rotation matrix space, so we use the following general formulas for three bodies in a chain base branch branch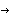 leaf. leaf.
basebranch 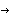 the rotation from the base coordinate system to the branch (a variable rotation) the rotation from the base coordinate system to the branch (a variable rotation)
baseleaf 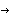 the rotation from the base coordinate system to the leaf (a variable rotation) the rotation from the base coordinate system to the leaf (a variable rotation)
branchleaf 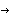 the rotation from the branch coordinate system to the leaf at neutral loading (a constant rotation) the rotation from the branch coordinate system to the leaf at neutral loading (a constant rotation)
delta* 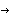 the rotational displacement in one of the three coordinate systems the rotational displacement in one of the three coordinate systems
then
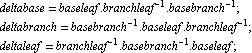
Note that the conversion of a list of Euler parameters to a virtual rotation vector could be done with VirtualRotation. However, the approximation used here (multiply by 2 and drop the first term) is very efficient and accurate for small displacements.
So, in the case of the right upper arm,
 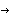 EulerParameters[bdrtupperarm] EulerParameters[bdrtupperarm]
 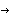 EulerInverse[EulerParameters[rtshoulderrot]] EulerInverse[EulerParameters[rtshoulderrot]]
 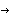 EulerInverse[EulerParameters[bdtorso]] EulerInverse[EulerParameters[bdtorso]] For the moments applied to the wrists, we will choose the local coordinate system for each moment and apply each moment separately to each body to achieve equal and opposite reactions. This choice will result in computational efficiency that is identical to what would be achieved by applying moments in global coordinates while modeling in global angular coordinates. In summary, applying loads in the same coordinate system as the modeling coordinate system is best. Applying loads in any coordinate system while modeling with Euler parameters is second best. Applying loads in the local or global coordinate systems while making the opposite choice for modeling coordinates ranks third. Finally, using local angular coordinates for modeling and then applying loads in the local coordinate system of a body other than the body to which the loads are applied is the worst because two full transformations are required for each load.
Finally, we apply a force of variable magnitude to the end of the golf club to see how it displaces the arms of the human. The magnitude of the applied force is set to zero and the loads are added to the model. Constrained Static SolutionFirst, we will solve for the static reaction forces with the current set of constraints. This gets us good initial guesses for the Lagrange multipliers. As a sanity check, we will show that all of our applied moments are in fact equal and opposite pairs by showing that the net force and moment applied to the feet is zero. Static EquilibriumNow build a FreeSystem object that will find the static equilibrium configuration without the unneeded constraints. Here we are removing all the constraints that restrict joint movement in the right arm, and the constraint that prevents elbow flapping in the left arm. Solve for the static equilibrium configuration of this system, which is now 8 DOF underconstrained. Note that the position of the golf club is now perfectly symmetric. This is because the applied loads are symmetric.
As a validity check, this shows that the reaction at the feet is zero because there are no external applied loads. If any of our independent moment specifications failed to provide equal and opposite reaction forces at a joint, then this would be nonzero. Now let us look at the configurations of the joints, relative to our initial guesses. First, we compare the elbow angle. Now we compare the shoulder displacement to its initial configuration. And here we compare the wrist displacement. Now we apply a force in the +X direction to the head of the golf club and solve for static equilibrium again. And now we can see the displacements at the wrists and shoulders that result from the load on the club.
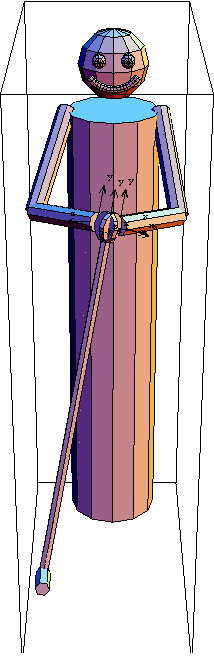  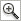
Again, we check that our reaction forces at the feet continue to make sense. The reaction vector matches the applied load at the head of the golf club. InverseDynamicsForward SolutionReturning to the fully constrained model, we can remove the load applied to the golf club and give the right wrist a nonzero angular velocity. This will allow us to find the reaction forces that result from forcing the golf club to follow a specified trajectory. The reaction forces at the feet no longer have predictable zero components because the acceleration of the golf club is nontrivial. FindRoot with Inverse DynamicsImagine now that we wish to find the trajectory of the golf club that will result in a specific set of reaction forces at the feet. Using the previous result as a guide to approximately where a solution might exist, we can easily use FindRoot to numerically seek a solution in n-dimensional space using the entire Modeler3D model as a black-box numerical function.
We wish to seek the values of two variables, omx and omy, that satisfy two criteria. Our two criteria will be to specify values for the X and Y components of the reaction force at the feet. First, we define a numerical function f that takes two arguments and returns a list of two numbers. FindRoot will seek values for the two numbers that result in the two return values being driven to zero. Here is the solution. A side effect of our function f is that the parameter values for omx and omy have already been set to the values returned by FindRoot. Check that we really achieved the desired result. SolveCouple with Inverse DynamicsWe can solve exactly the same problem with the Modeler3D functions SetCouple and SolveCouple. Mathematically speaking, the SetCouple method is more elegant because it produces a new system of equations representing the static equilibrium model with two new variables--it solves one complete numerical model instead of seeking a numerical solution to a black-box model that is, itself, another numerical model. However, elegance doesn't always pay off. The SolveCouple method is faster than FindRoot, but the cost of building the new system of derivatives required by SetCouple is extremely high. Which is really better depends on how many times you plan to run the model versus how many times you must rebuild it. And here is the solution. Check that we achieved the same result. Why does it take so long to create cpsys? This might hold a clue to the answer. End
|