Front Suspension

MechanicalSystems Model of a Transverse-Shock, Anti-Roll Automotive Front Suspension

by Robert Beretta

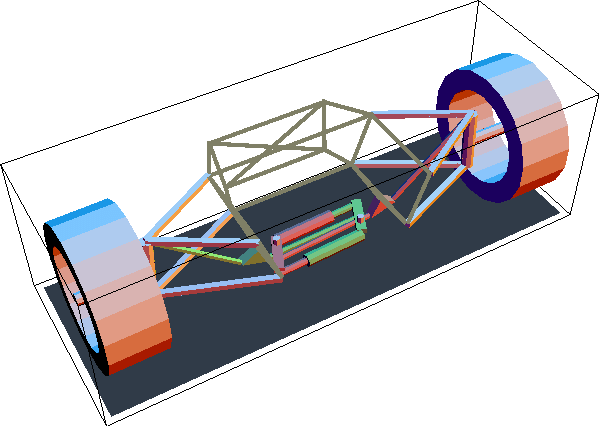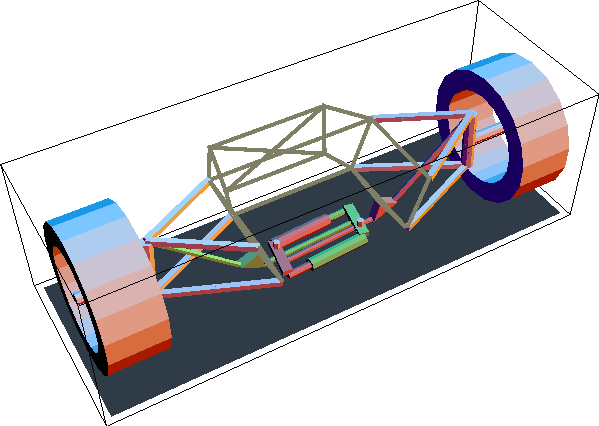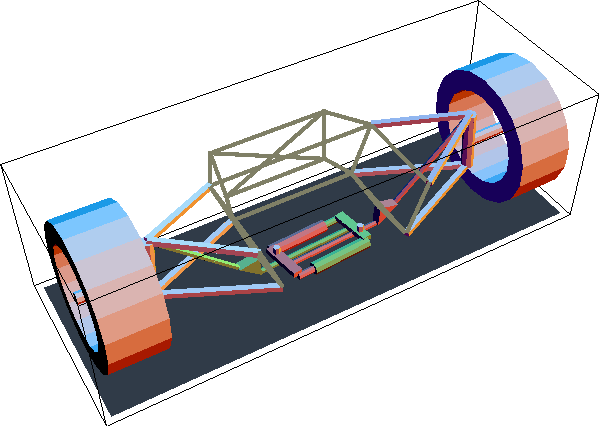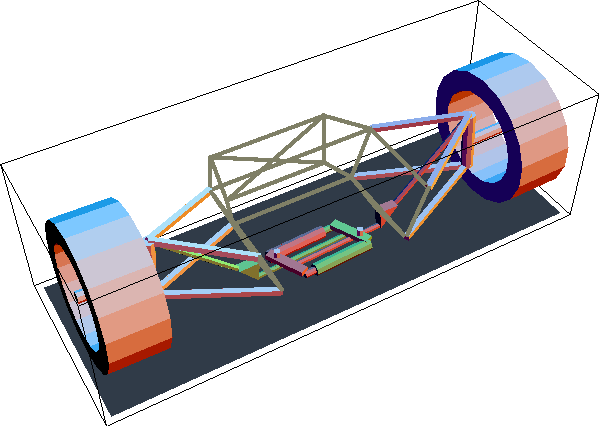
Suspension Animation

Discussion

Suspension Function

This notebook describes the motion of a pull-rod, inboard-damper, automotive front suspension system. The suspension system is analyzed to show how changes in the linkage geometry affect the velocity ratio between wheel and damper motion. A static force analysis is done to determine the loads on each of the elements of the suspension linkage.

The pull-rod front suspension mechanism is a rising-rate, inboard-damper, automotive suspension system that has inherent anti-roll characteristics. Its function is described as follows.

The wheel carrier is primarily attached to the chassis by a classic double A-arm. A primary tie rod attaches to the top of the wheel carrier and extends downward toward the center and bottom of the car, such that it is in tension when supporting the weight of the car. This tie rod is attached to the rocker arm, which is forced to pivot about its axis on the chassis as the suspension travels.

As the rocker arm pivots it pulls on the secondary tie rod, which passes from the rocker arm across the bottom of the car to the toggle. Thus, the right-hand wheel directly actuates the left toggle, and vice-versa.

The two damper-spring assemblies (shocks absorbers) lie horizontally across the bottom of the vehicle, one in front of the other. Thus, the suspension is asymmetrical in the vehicle, although its operation is symmetrical with respect to the compression of the shocks relative to wheel travel. Each of the two shocks attaches to both of the toggles, being controlled simultaneously from both ends. If one wheel were to go over a bump, while the other stayed still, the rotation of the toggle attached to that wheel would cause one of the two shocks to be compressed, and the other shock to be released.

The unique anti-roll characteristics of this suspension system can be described qualitatively as follows.

Imagine that the end of each toggle that compresses the shock is three times longer than the end that releases the shock. The vehicle then goes over a bump that moves both wheels upward simultaneously 1 unit of travel. Call it a 1-unit bump. The compression end of each toggle compresses its shock 3 units, while the release end of each toggle releases its shock 1 unit. This results in a net compression of each shock of 2 units.

Now imagine that the vehicle is rolling in a corner such that the right wheel travels upward 1 unit, and the left wheel travels downward 1 unit. The toggle associated with the right wheel compresses its shock 3 units, while the toggle associated with the left wheel compresses the same shock 1 more unit, for a total compression of 4 units. Similarly, the other shock is released 4 units by the chassis roll.

To summarize, a 3:1 ratio between the length of the compression and release ends of the toggles results in effective suspension stiffness that is two times greater in pure roll than in pure bump. The magnification of the anti-roll characteristic is adjusted simply by changing the ratio of the lengths of the two ends of the toggles.

Suspension Model

Bodies

The Modeler3D model of the inboard-damper suspension consists of six bodies, five of them moving:
1. The ground--this body serves as the stationary reference frame for the entire model.
2. The chassis
3. The right carrier--since the wheel does not need to spin in this model, this single body serves as both the right wheel and right wheel carrier (the king pin).
4. The left carrier--this body serves as the left wheel and left wheel carrier.
5. The right rocker--the rocker arm that links the two tie rods for the right suspension.
6. The left rocker--the rocker arm that links the two tie rods for the left suspension.
7. The left toggle--the final rocker arm that ties the motion of the right wheel to its shock.
8. The right toggle--the final rocker arm that links the motion of the left wheel to its shock.

Coordinates

The 3D coordinate system of the model is as follows.
+X is out the back of the vehicle.
+Y is out the right side of the vehicle.
+Z is straight up.

The origin of the global coordinate system is located on the surface of the ground (Z), at the center of the car (Y), and directly between the centers of the two front wheels (X). All units are assumed to be in inches. The overall physical scale of the model is that of a 3/4 scale Formula One car.

Kinematic Model

Preparation

This loads the required Modeler3D package into Mathematica.

Names are defined for each of the body numbers for clarity.

Useful named vectors.

Body Definitions

Ground

Two points are defined on the ground (body 1).
P1. A point directly above the origin (+Z direction) to define a vertical translation axis for the chassis.
P2. A point directly to the right side of the origin (+Y direction) to use as a rotational orientation reference for the chassis.

Chassis

The local origin of the chassis is located at the bottom surface of the chassis, at the center of the car, directly below the wheel axis. Thus, the origin of the chassis is coincident with the origin of the ground when the car's suspension is bottomed out.

Sixteen points are defined on the chassis (body 2).
P1. The center of rotation of the right upper A-arm on the chassis. The upper ball joint on the right wheel carrier travels on a circular path centered at this point.
P2 and P3. The two attachment points of the right upper A-arm on the chassis. These are immediately in front of and behind point P1.
P4. The center of rotation of the left upper A-arm on the chassis. This point is mirrored from point 1 across the plane normal to the local Y axis.
P5 and P6. The two attachment points of the left upper A-arm on the chassis. These are immediately in front of and behind P4.
P7. The center of rotation of the right lower A-arm on the chassis. The lower ball joint on the right wheel carrier travels on a circular path centered at this point.
P8 and P9. The two attachment points of the right lower A-arm on the chassis. These are immediately in front of and behind P7.
P10. The center of rotation of the left lower A-arm on the chassis. This point is mirrored from P7.
P11 and P12. The two attachment points of the left lower A-arm on the chassis. These are immediately in front of and behind P10.
P13. A point on the pivot axis of the right rocker on the chassis.
P14. A point on the pivot axis of the left rocker on the chassis.
P15. A point on the pivot axis of the right toggle on the chassis. The Z coordinate of this point sets the height of the center-line of the right toggle.
P16. A point on the pivot axis of the left toggle on the chassis.

The InitialGuess for the chassis corresponds to the chassis being 1.5 inches off of the ground (normal ride height). Only the mass of the chassis is included in this model because the masses of the other components are negligible.

Right and left carriers

The local origins of the two wheel carriers are at the attachment points of the lower A-arms.

Four points are defined on each wheel carrier (bodies 3 and 4).
P1. The attachment point of the upper A-arm on the carrier.
P2 and P3. Two points that define the ends of the axle on the wheel carrier.
P4. A point at the bottom of the tire, where the tire touches the ground. This point is used to constrain the bottom of the tire to be in contact with the ground.
P5. A point at the end of the axle that is used to simplify the definitions of the graphics objects.

The points on the left wheel carrier are a mirror of the points on the right wheel carrier, mirrored across the local Y plane relative to the right wheel carrier.

Right and left rockers

The local origins of the rockers are located at the points where they attach to the chassis.

Two points are defined on each rocker (bodies 5 and 6).
P1. The attachment point of the upper tie rod on the rocker.
P2. The attachment point of the lower tie rod on the rocker.

The left rocker is a mirror of the right rocker.

SetParameters is used to set the value of a constant in the model; in this case the value of RockerLength.

Right and left toggles

The local origins of the toggles are located at the points where they attach to the chassis.

Three points are defined on each toggle (bodies 7 and 8).
P1. The attachment point of the shock absorber that is extended during bump.
P2. The attachment point of the lower tie rod on the toggle.
P3. The attachment point of the shock absorber that is compressed during bump.

The left toggle is a mirror of the right toggle.

Build bodies

SetBodies incorporates the body objects into the current model.

Constraint definitions

Constraints for the chassis

1. A translational joint to allow the chassis to translate on a plane that is normal to the global X axis.
2. A relative Y constraint to control the side-to-side position of the car.
3. A relative Z constraint to set the height of the chassis by specifying the Z component of the origin of the chassis. Positive T causes the car to move towards the ground, T = 0 is equal to 1.5 inch ride height.
4. A relative angle constraint to control the roll of the car. Positive T causes the car to roll to the left.

Driving constraints 3 and 4 can be turned "on and off" by setting the values of Roll and Bounce equal to 0 or 1.

Constraints for the right and left carriers

5. A constraint to model the right upper A-arm. Two degrees of freedom constrained.
6. A constraint to model the right lower A-arm. Two degrees of freedom constrained.
7. A constraint to set the steering angle of the right wheel by controlling the included angle between the axle and a fore-aft line on the ground. One degree of freedom constrained.
8. A constraint to place the bottom of the right tire on the surface of the road. One degree of freedom constrained.

Constraints 9, 10, 11, and 12 control the left wheel carrier in a similar fashion.

Constraints for the right and left rockers

13. A revolute constraint to model the pivot axis of the right rocker. Five degrees of freedom constrained.
14. A constraint to model the right upper-right tie rod. One degree of freedom constrained.
15. A revolute constraint to model the pivot axis of the left rocker. Five degrees of freedom constrained.
16. A constraint to model the left upper-left tie rod. One degree of freedom constrained.

Constraints for the left and right toggles

17. A constraint to model the lower-right tie rod. One degree of freedom constrained.
18. A revolute constraint to model the pivot axis of the left toggle. Five degrees of freedom constrained.
19. A constraint to model the lower-left tie rod. One degree of freedom constrained.
20. A revolute constraint to model the pivot axis of the left toggle. Five degrees of freedom constrained.

Build constraints

Any subset of the entire set of defined constraints may be used, so long as the set adequately constrains some subset of the bodies in the mechanism.

Set 1: Constrain the chassis only.

Set 2: Constrain the chassis and right carrier.

Set 3: Constrain the chassis and left and right carriers.

Set 4: Constrain the chassis and right carrier and rocker.

Set 5: Constrain everything but the right toggle.

Set 6: Constrain all bodies.

Running the model

CheckSystem

CheckSystem tests for certain mathematical errors. A return value of True means that no errors were found.

SolveMech

SolveMech[t] seeks a solution that satisfies all of the constraints with the value of time T set to t. The solution is returned as a list of rules specifying the position of the origin of each body and the Euler parameters Eo, Ei, Ej, and Ek that uniquely specify the angular orientation of each body.

Output Functions

The length of the shock absorber is equal to the distance between the ends of the two toggles. The following function returns the left and right shock lengths as functions of the model's dependent variables. The right shock is defined as the shock that gets compressed when the right wheel bumps. In point of fact, the right shock is the rear shock.

Both shocks are the same length in bounce.

The degree of CCW body roll that would provide left and right wheel bounce of 0.25 and -0.25 inches, respectively, is calculated as follows.

Shock lengths differ with 1 degree of body roll to the left.

It can be seen that body roll induces greater deflection of the shocks than does an equivalent degree of bounce.

Velocity solution

The following calculates the length of the shock at ride height, and the rate of change of the length of the shock at ride height, with respect to changes in time T. The negative rate of change implies that the shock is getting shorter as the car bounces. The

Tabular Output

Variations in time

Tables of solution points can be created using SolveMech. These tables can then be used to generate plots of various functions versus time.

SetBodies is first called with no arguments to reset all of the initial guesses to the values defined previously in their respective Body objects. SolveMech is then used to move the initial guesses up to top-out in 2 steps.

SolveMech uses a special form of iterator: the following input causes SolveMech to generate 11 solution points, with values of time varying from -1.0 to 1.5; top-out to full bounce.

Plot of wheel to shock leverage ratio as a function of bump height.
This plot shows that this suspension is a "rising rate" suspension.

Plot of shock length as a function of bump height.

Plot of camber angle as a function of bump height.

Plot of tire scrub as a function of bump height.

Variations in Rocker Length

To create a table of solution points while varying some parameter other than time, the Mathematica Table function is used.

Plot of wheel to shock leverage as a function of rocker length, with bump held constant at zero.

Graphic Images

Graphic Objects

Here is a graphic object of the chassis and ground plane.

Here is a graphic objects of wheel carriers.

Here is a graphic objects of right and left rockers.

Here is a graphic object of left and right toggles.

Graphics Displays

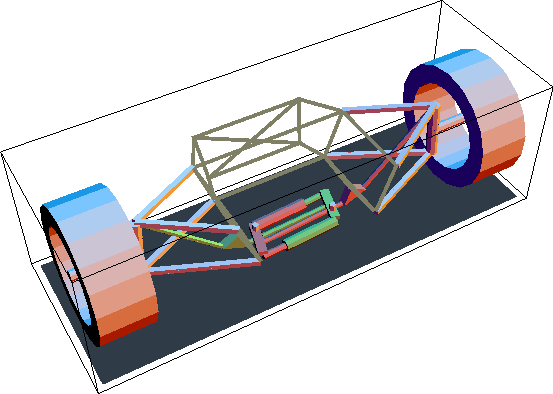
The following input was used to create the animation sequence at the beginning of this notebook.

Static Loads

Loads are applied to the model to simulate the shock absorbers. Load 1 models the right shock spring, with a specified spring free length and spring rate. Load 2 models the left shock spring.

SetLoads applies the load objects to the model.

The following two inputs return the reaction forces that the ground applies to the bottom of each tire at ride height; the ground is pushing up on each tire with 99 pounds of force.

Reaction[8, rightcarrier] returns the reaction forces that constraint number 8 applies to the right wheel carrier.

Since there are not, as yet, any gravitational loads applied to the chassis, the vertical driving constraint (constraint 3) must apply a 197-pound downward load to the chassis, to counter the 98-pound upward force on each tire.

A load representing gravity is added so that the equilibrium position of the chassis can be found. The mass of the chassis was already defined in the chassis Body object. Total weight on front of car is 193.2 pounds.

The gravitational loads now almost balance the suspension loads. Constraint 3 is the constraint that controls the vertical motion of the chassis.

Constraint 4 is the constraint that controls the roll of the chassis. There is no load on this constraint because the chassis loading is symmetrical.

Two loads representing the side loads induced by a right-hand corner are added to the bottom of each tire. The magnitude of the side load on each tire is proportional to the normal force on the tire, representing kinetic friction. This condition would probably only exist during a slide, but the normal case is indeterminate, so this has to do.

Equilibrium

A FreeSystem is built that has had constraints 3 and 4 dropped, the constraints that control the vertical position and the rotation of the chassis. This allows the chassis to move to its equilibrium position.

The following generates spurious errors in Version 5.0.1 because of changes to LinearSolve.

The car is in equilibrium at a ride height of 1.5339 inches.

There is no chassis roll in this load state.

The car is now put into a 1-G right-hand turn.

The following generates spurious errors in Version 5.0.1 because of changes to LinearSolve.

The ride height of the car has gone up a bit.

0.22 degrees of body roll to the left.

Component Loads

Note that all of the following loads are based on the results of the 1-G right-hand corner equilibrium calculation.

Here are the load vectors, in global coordinates, applied to the right and left wheel carrier upper A-arm attachment points by the upper A-arms.

Here are the load vectors applied to the right and left wheel carrier upper A-arm attachment points by the upper tie rods.

Here are the magnitudes of the tensile forces in the right and left upper tie rods.

Here are the load vectors, in global coordinates, applied to the right and left wheel carrier lower A-arm attachment points by the lower A-arms.

Here are the magnitudes of the tensile forces in the right and left lower tie rods.

Here are the load vectors, in global coordinates, applied to the right and left toggles by the chassis, at their pivot axes on the chassis.

Here are the loads in the right and left shocks.

Other Forces

End