1.2.4 Running the ModelA single command is used to solve the constraint equations and return a list of rules representing the coordinates of each body in the model. The fundamental model-solving function. This seeks a solution at crankangle = 0.
Out[8]= |  |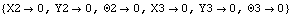
SolveMech returns the global coordinates of the origin of each body in the system. The symbols X2 and Y2 specify the location of the origin of body 2, the crankshaft, and  2 specifies the rotation of the crankshaft. SolveMech returns a 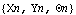 triplet for each body in the system. A graphic of the model at crankangle = 0.
Big surprise! The trivial solution at crankangle = 0 corresponds to the local coordinate system of each body being aligned with the global coordinate system. This is because the model was defined such as to have this perfect assembled configuration. The piston is defined such that its local origin lies at a point that is outside of the piston body, directly on the global origin when crankangle = 0. Note also the 3-4-5 triangle formed by the crankshaft, piston, and connecting rod when crankangle = 0.
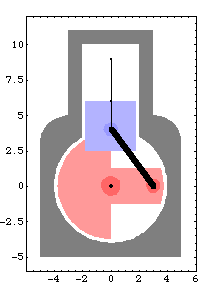
Advancing crankangle results in a more interesting solution. This seeks a solution at crankangle = 1/10 revolution.
Out[10]= |  |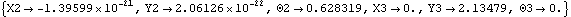
Now the angular coordinate of the crankshaft, 2, has advanced to 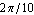 , as specified, and the vertical coordinate of the piston, Y3, has increased to 2.13. All of the other coordinates are still zero and will always be so because of the specific function of this mechanism model. This seeks a solution at crankangle = 3/10 revolution.
Out[12]= |  |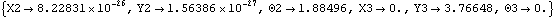
A graphic of the model at crankangle = 3/10 revolution.
| 
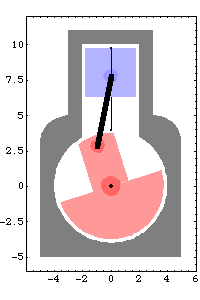
