1.3 Basic 3D Model

In this section the basic functionality of Modeler3D is demonstrated by building a kinematic model of a very simple mechanism. The mechanism is a slider-crank mechanism with two moving bodies, the crankshaft and the piston, identical to the mechanism that was modeled with Modeler2D in Section 1.2. Even though it is simply a planar mechanism, the slider-crank is modeled with Modeler3D to demonstrate the parallelism between Modeler2D and Modeler3D.

1.3.1 Mechanism Function

The Modeler3D package must be loaded before calling any Modeler3D functions.

This loads the Modeler3D package.

In[1]:=

Here is a graphic of the 3D slider-crank model.

The following example analyzes the motion of a classic slider-crank mechanism. This mechanism is modeled with a simple and intuitive set of mechanical constraints that are representative of how such a problem would usually be modeled with Modeler3D.

Body Numbers

Each independent body in a Mech model must be given a unique positive integer body number. The choice of each body number is arbitrary except for the ground body, which must be body 1. These body numbers are used throughout a Mech model to reference each body. The ground body, which is stationary by definition, is used as the reference location and orientation for the rest of the model. All mechanism models must have some reference to the ground body to be adequately constrained.
To aid in the readability of the mechanism models created with Mech, it is customary to name each of the bodies in a mechanism, and then define each of these names to be equal to the integer body number of the body. Each body can then be referenced by name instead of by a number.

Define body names to be used to reference each body.

In[2]:=

A real slider-crank mechanism would have a fourth body; the connecting rod between the crankshaft and the piston. However, in the kinematic model this entire part can be replaced by a simple distance constraint specifying that the crank pin and the piston pin are to be a constant distance apart. This technique decreases the overall size of the model.

Local Coordinates

Each body in a mechanism model must have a local coordinate system attached to it. How to place this coordinate system on the body is up to the user and is based on the needs of the model. It is not necessary to place the local coordinate origin at the center of gravity of the body. The local coordinate system of each body is used to define points, lines, planes, and other features on the body that are then tied together to make the mechanical constraints.
The local coordinate system of the ground body is coincident with the global coordinate system. Therefore, the global coordinate system is referenced only through the ground body by specifying body 1.

1.3.2 3D Bodies

Ground

The local coordinate system of the ground body originates at the center of the crankshaft.

Here is a graphic of the ground body. The point coordinates on the ground body are P1 {0, 0, 0}, P2 {0, 0, 5}, P3 {3, 0, 0}, P4 {0, 4, 0}, and P5 {0, 9, 0}.

Crankshaft

The local coordinate system of the crankshaft originates at its rotational center.

Here is a graphic of the crankshaft. The local point coordinates on the crankshaft are P1 {0, 0, 0}, P2 {0, 0, 5}, and P3 {3, 0, 0}.

Piston

The local coordinate system on the piston originates at a point that is four units below the attachment point of the connecting rod. Thus, when the slider-crank mechanism is in its initial configuration, the local origin of the piston is coincident with the global origin.

Here is a graphic of the piston. The local point coordinates on the piston are P1 {0, 4, 0}, P2 {0, 6, 0}, and P3 {0, 4, 5}.

1.3.3 3D Constraints

Now that the local point coordinates on each 3D body are defined, building the model is simply a matter of tying the points together with the correct mechanical constraints. Modeler3D provides a library of mechanical constraint objects that translate the desired physical conditions that are imposed on the model into mathematical equations.

Constraint Objects

Five constraint objects are used to model the slider-crank mechanism, constraining a total of 12 degrees of freedom (6 degrees of freedom for each moving body).

Some 3D constraint objects.

Note that the last character in the name of any Mech constraint object is an integer that specifies the number of degrees of freedom that it constrains.
The first argument to each constraint object, cnum, is the user-specified constraint number. This number is used to reference the constraint later in the modeling process, just as body numbers are used to reference specific bodies.
The point, vector, and axis arguments required by Modeler3D constraint objects are specified with Point, Vector, Line, Axis, and Plane objects, used in much the same manner as the built-in Mathematica graphics primitives, Point and Line. These objects are discussed in detail in Section 2.2.

Building the Model

The Modeler3D constraint objects used to model the physical relationships in the slider-crank model are as follows.

The Modeler3D constraint objects are finally assembled into a mechanism model with SetConstraints.

The fundamental model-building function.

Here is the entire slider-crank model built in one step.

In[5]:=

SetConstraints returns Null. All of the mechanism equations generated by SetConstraints are stored internally in the Modeler3D private context.

1.3.4 Running the Model

A single command is used to solve the constraint equations and return the coordinates of each of the bodies the model.

The fundamental model-solving function.

This seeks a solution at crankangle = 0.

In[7]:=

Out[8]=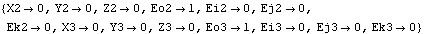

SolveMech returns the global coordinates of the origin of each body in the system. X2, Y2, and Z2 specify the location of the origin of body 2, the crankshaft.
Eo2, Ei2, Ej2, and Ek2 are the Euler generalized parameters specifying the angular orientation of the crankshaft. SolveMech returns a {Xn, Yn, Zn, Eon, Ein, Ejn, Ekn} set for each body in the system. For those unfamiliar with Euler parameters, suffice it to say that the four Euler parameters provide a numerically robust means of specifying the three degrees of freedom of the angular orientation of a body in 3D space. Values of {1, 0, 0, 0} for the four parameters, respectively, correspond to alignment with the global coordinate system. It is not necessary to have an understanding of the Euler parameters to utilize Modeler3D because postprocessing functions use the Euler parameters to generate more familiar output, such as the rotation of a body about an axis or the angle between two vectors. Euler parameters are discussed further in Chapter 4.

Here is a graphic of the slider-crank model at the initial configuration.

Not a very interesting solution! The solution at crankangle = 0 is for the local coordinate system of each body to be aligned with the global coordinate system. This is because the model was defined such as to have this perfect assembled configuration. The piston is defined such that its local origin lies at a point that is outside of the piston body. This point is coincident with the global origin when crankangle = 0. Note the 3-4-5 triangle formed by the crankshaft, piston, and connecting rod when crankangle = 0.
Advancing crankangle results in a more interesting solution.

This seeks a solution at crankangle = 1/10 revolution.

In[9]:=

Out[10]=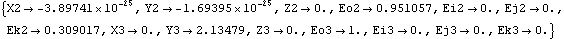

Now two of the Euler parameters of the crankshaft Eo2 and Ek2 have changed, and the vertical coordinate of the piston Y3 has increased to 2.13. All of the other coordinates have not changed, and never will, because of the specific function of this particular mechanism model.

This seeks a solution at crankangle = 3/10 revolution.

In[11]:=

Out[12]=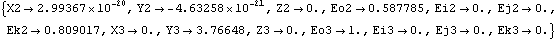

Here is a graphic of the model at crankangle = 3/10 revolution.

Undocumented Graphics Generation

The following code generates the graphics in this section. These Modeler3D commands are defined in Chapter 3.