1.2 Basic 2D Model

In this section the basic functionality of the Modeler2D package is demonstrated by building a kinematic model of a very simple mechanism. The mechanism is a planar slider-crank mechanism with two moving bodies, the crankshaft and the piston. The mechanism is modeled using the most abbreviated technique possible with Modeler2D. Later chapters will delve into the many more complex variations on these techniques.

1.2.1 Mechanism Function

The Modeler2D package must be loaded before calling any Mech functions.

This loads Modeler2D.

In[1]:=

Here is a graphic of the 2D slider-crank model.

The following example analyzes the motion of a classic slider-crank mechanism. This mechanism is modeled with a simple and intuitive set of mechanical constraints that are representative of how such a problem would usually be modeled.

Body Numbers

Each independent body in a Mech model must be given a unique positive integer body number. The choice of each body number is arbitrary, except for the ground body, which must be body 1. These body numbers are used throughout a Mech model to reference each body. The ground body, which is stationary by definition, is used as the reference location and orientation for the rest of the model. All mechanism models must have some reference to the ground body to be adequately constrained.
To aid in the readability of the mechanism models created with Mech, a good practice is to name each of the bodies in a mechanism, and then define each of these names to be equal to the integer body number of the body. Each body can then be referenced by name instead of by a number.

Body names are defined to be used as references for each body.

In[2]:=

A real slider-crank mechanism would have a fourth body, the connecting rod between the crankshaft and the piston. However, in the kinematic model this entire part can be replaced by a simple distance constraint specifying that the crank pin and the piston pin are a constant distance apart. This technique decreases the overall size of the model.

Local Coordinates

Each body in a mechanism model must have a local coordinate system attached to it. How to place this coordinate system on the body is up to the user and is based on the needs of the model. It is not necessary to place the local coordinate origin at the center of gravity of the body. The local coordinate system of each body is used to define points, lines, and other features on the body that are then tied together to make the mechanical constraints.
The local coordinate system of body 1, the ground body, is always coincident with the global coordinate system. Therefore, the global coordinate system is referenced through the ground body, simply by specifying body 1.

1.2.2 2D Bodies

Ground

The local coordinate system of the ground body originates at the rotational center of the crankshaft.

Here is a graphic of the ground body.

Crankshaft

The local coordinate system of the crankshaft originates at its rotational center.

Here is a graphic of the crankshaft.

Piston

The local coordinate system of the piston originates four units below the attachment point of the connecting rod. Thus, when the mechanism is in its initial configuration, the local origin of the piston is coincident with the global origin.

Here is a graphic of the piston.

1.2.3 2D Constraints

Now that the local point coordinates on each body are defined, building the model is simply a matter of tying the points together with the correct mechanical constraints. Modeler2D provides a small library of mechanical constraint objects that translate desired physical conditions that are imposed on the model into mathematical equations.

Constraint Objects

Four constraint objects are used to model the slider-crank mechanism, constraining a total of six degrees of freedom (three degrees of freedom for each moving body).

Some 2D constraint objects.

Note that the last character in the name of any Mech constraint object is an integer that specifies the number of degrees of freedom that it constrains.
The first argument to each constraint object, cnum, is the user-specified constraint number. This number is used to reference the constraint later in the modeling process, much like body numbers are used to reference specific bodies.
The point and axis arguments of Modeler2D constraint objects are specified with Point, Line, or Axis objects, used in much the same manner as the built-in Mathematica graphics primitives Point and Line. These objects are discussed in detail in Section 2.2.

Building the Model

The Modeler2D constraint objects used to model the physical relationships in the slider-crank mechanism are as follows.

A Revolute2 constraint forces the axis of the crankshaft to be coincident with the global origin. This constrains the X and Y displacement of the crankshaft axis. The one degree of freedom left for the crankshaft is its rotation about its axis. The syntax of the constraint can be interpreted as, "Constrain a point at on the ground body to be coincident with point on the crankshaft."

The Modeler2D constraint objects are finally assembled into a mechanism model with SetConstraints.

The fundamental model-building function.

Here is the entire slider-crank model built in one step.

In[5]:=

SetConstraints returns nothing upon success. All of the constraint equations generated by SetConstraints are stored internally in the Modeler2D private context.

1.2.4 Running the Model

A single command is used to solve the constraint equations and return a list of rules representing the coordinates of each body in the model.

The fundamental model-solving function.

This seeks a solution at crankangle = 0.

In[7]:=

Out[8]=

SolveMech returns the global coordinates of the origin of each body in the system. The symbols X2 and Y2 specify the location of the origin of body 2, the crankshaft, and 2 specifies the rotation of the crankshaft. SolveMech returns a triplet for each body in the system.

A graphic of the model at crankangle = 0.

Big surprise! The trivial solution at crankangle = 0 corresponds to the local coordinate system of each body being aligned with the global coordinate system. This is because the model was defined such as to have this perfect assembled configuration. The piston is defined such that its local origin lies at a point that is outside of the piston body, directly on the global origin when crankangle = 0. Note also the 3-4-5 triangle formed by the crankshaft, piston, and connecting rod when crankangle = 0.
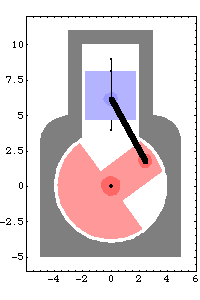
Advancing crankangle results in a more interesting solution.

This seeks a solution at crankangle = 1/10 revolution.

In[9]:=

Out[10]=

Now the angular coordinate of the crankshaft, 2, has advanced to , as specified, and the vertical coordinate of the piston, Y3, has increased to 2.13. All of the other coordinates are still zero and will always be so because of the specific function of this mechanism model.

This seeks a solution at crankangle = 3/10 revolution.

In[11]:=

Out[12]=

A graphic of the model at crankangle = 3/10 revolution.

Undocumented Graphics Generation

The following code generates the graphics in this section. These Modeler2D commands are defined in Chapter 3.